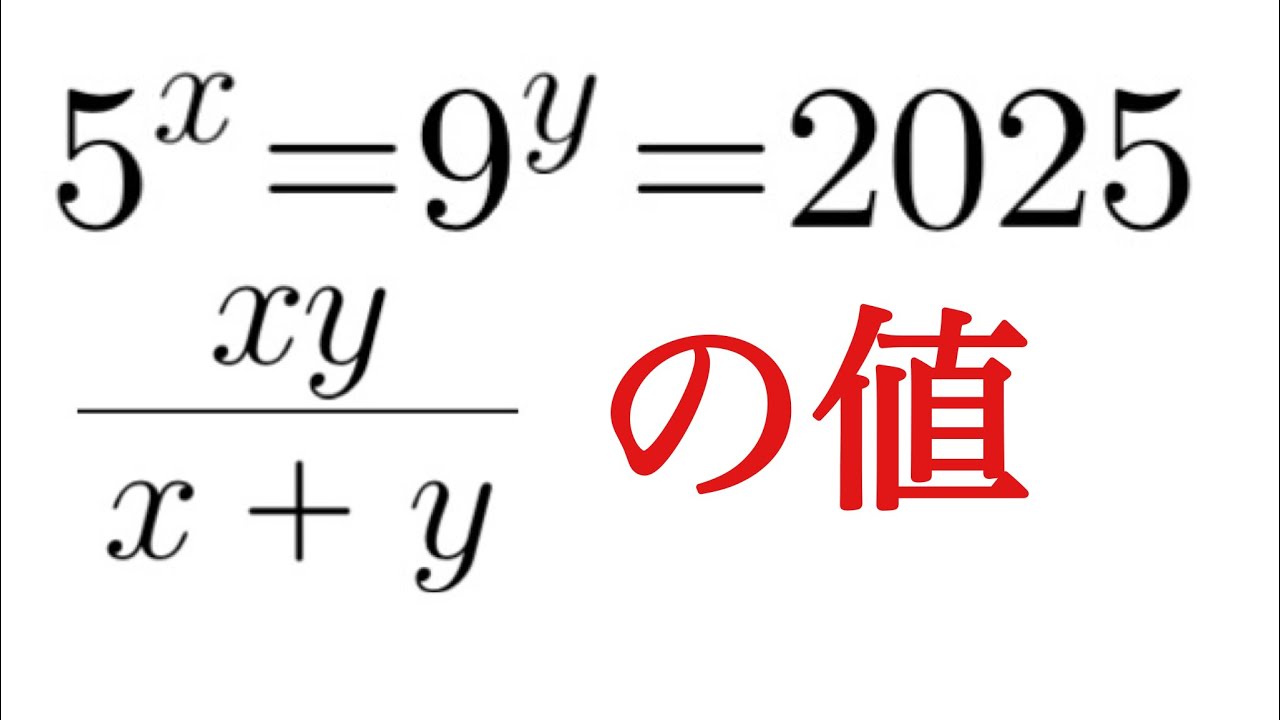問題文全文(内容文):
[2]a,bは正の実数であり、$a\neq 1,b\neq 1$を満たすとする。太郎さんは
$\log_ab$と$\log_ba$の大小関係を調べることにした。
(1)太郎さんは次のような考察をした。
まず、$\log_39=\boxed{\ \ ス\ \ }, \log_93=\frac{1}{\boxed{\ \ ス\ \ }}$である、この場合
$\log_39 \gt \log_93$
が成り立つ。
一方、$\log_{\frac{1}{4}}\boxed{\ \ セ\ \ }=-\frac{3}{2},\log_{\boxed{セ}}\frac{1}{4}=-\frac{2}{3}$である。この場合
$\log_{\frac{1}{4}}\boxed{\ \ セ\ \ } \lt \log_{\boxed{セ}}\frac{1}{4}$
が成り立つ。
(2)ここで
$\log_ab=t \ldots①$
とおく。
(1)の考察をもとにして、太郎さんは次の式が成り立つと推測し、
それが正しいことを確かめることにした。
$\log_ba=\frac{1}{t} \ldots②$
①により、$\boxed{\ \ ソ\ \ }$である。このことにより$\boxed{\ \ タ\ \ }$が得られ、②が
成り立つことが確かめられる。
$\boxed{\ \ ソ\ \ }$の解答群
$⓪a^k=t ①a^t=b ②b^a=t$
$③b^t=a ④t^a=b ⑤t^b=a$
$\boxed{\ \ タ\ \ }$の解答群
$⓪a=t^{\frac{1}{b}} ①a=b^{\frac{1}{t}} ②b=t^{\frac{1}{a}}$
$③b=a^{\frac{1}{t}} ④t=b^{\frac{1}{a}} ⑤t=a^{\frac{1}{b}}$
(3)次に、太郎さんは(2)の考察をもとにして
$t \gt \frac{1}{t} \ldots③$
を満たす実数$t(t\neq 0)$の値の範囲を求めた。
太郎さんの考察
$t \gt 0$ならば、③の両辺にtを掛けることにより、$t^2 \gt 1$を得る。
このような$t(t \gt 0)$の値の範囲は$1 \lt t$である。
$t \lt 0$ならば、③の両辺にtを掛けることにより、$t^2 \lt 1$を得る。
このような$t(t \lt 0)$の値の範囲は$-1 \lt t \lt 0$である。
この考察により、③を満たす$t(t\neq 0)$の値の範囲は
$-1 \lt t \lt 0, 1 \lt t$
であることが分かる。
ここで、aの値を一つ定めたとき、不等式
$\log_ab \gt \log_ba \ldots④$
を満たす実数$b(b \gt 0, b\neq 1)$の値の範囲について考える。
④を満たすbの値の範囲は$a \gt 1$のときは$\boxed{\ \ チ\ \ }$であり、
$0 \lt a \lt 1$のときは$\boxed{\ \ ツ\ \ }$である。
$\boxed{\ \ チ\ \ }$の解答群
$⓪0 \lt b \lt \frac{1}{a}, 1 \lt b \lt a ①0 \lt b \lt \frac{1}{a}, a \lt b$
$②\frac{1}{a} \lt b \lt 1, 1 \lt b \lt a ③\frac{1}{a} \lt b \lt 1, a \lt b$
$\boxed{\ \ ツ\ \ }$の解答群
$⓪0 \lt b \lt a, 1 \lt b \lt \frac{1}{a} ①0 \lt b \lt a, \frac{1}{a} \lt b$
$②a \lt b \lt 1, 1 \lt b \lt \frac{1}{a} ③a \lt b \lt 1, \frac{1}{a} \lt b$
(4)$p=\frac{12}{13}, q=\frac{12}{11}, r=\frac{14}{13}$とする。
次の⓪~③のうち、正しいものは$\boxed{\ \ テ\ \ }$である。
$\boxed{\ \ テ\ \ }$の解答群
$⓪\log_pq \gt \log_qp$かつ$\log_pr \gt \log_rp$
$①\log_pq \gt \log_qp$かつ$\log_pr \lt \log_rp$
$②\log_pq \lt \log_qp$かつ$\log_pr \gt \log_rp$
$③\log_pq \lt \log_qp$かつ$\log_pr \lt \log_rp$
2022共通テスト数学過去問
[2]a,bは正の実数であり、$a\neq 1,b\neq 1$を満たすとする。太郎さんは
$\log_ab$と$\log_ba$の大小関係を調べることにした。
(1)太郎さんは次のような考察をした。
まず、$\log_39=\boxed{\ \ ス\ \ }, \log_93=\frac{1}{\boxed{\ \ ス\ \ }}$である、この場合
$\log_39 \gt \log_93$
が成り立つ。
一方、$\log_{\frac{1}{4}}\boxed{\ \ セ\ \ }=-\frac{3}{2},\log_{\boxed{セ}}\frac{1}{4}=-\frac{2}{3}$である。この場合
$\log_{\frac{1}{4}}\boxed{\ \ セ\ \ } \lt \log_{\boxed{セ}}\frac{1}{4}$
が成り立つ。
(2)ここで
$\log_ab=t \ldots①$
とおく。
(1)の考察をもとにして、太郎さんは次の式が成り立つと推測し、
それが正しいことを確かめることにした。
$\log_ba=\frac{1}{t} \ldots②$
①により、$\boxed{\ \ ソ\ \ }$である。このことにより$\boxed{\ \ タ\ \ }$が得られ、②が
成り立つことが確かめられる。
$\boxed{\ \ ソ\ \ }$の解答群
$⓪a^k=t ①a^t=b ②b^a=t$
$③b^t=a ④t^a=b ⑤t^b=a$
$\boxed{\ \ タ\ \ }$の解答群
$⓪a=t^{\frac{1}{b}} ①a=b^{\frac{1}{t}} ②b=t^{\frac{1}{a}}$
$③b=a^{\frac{1}{t}} ④t=b^{\frac{1}{a}} ⑤t=a^{\frac{1}{b}}$
(3)次に、太郎さんは(2)の考察をもとにして
$t \gt \frac{1}{t} \ldots③$
を満たす実数$t(t\neq 0)$の値の範囲を求めた。
太郎さんの考察
$t \gt 0$ならば、③の両辺にtを掛けることにより、$t^2 \gt 1$を得る。
このような$t(t \gt 0)$の値の範囲は$1 \lt t$である。
$t \lt 0$ならば、③の両辺にtを掛けることにより、$t^2 \lt 1$を得る。
このような$t(t \lt 0)$の値の範囲は$-1 \lt t \lt 0$である。
この考察により、③を満たす$t(t\neq 0)$の値の範囲は
$-1 \lt t \lt 0, 1 \lt t$
であることが分かる。
ここで、aの値を一つ定めたとき、不等式
$\log_ab \gt \log_ba \ldots④$
を満たす実数$b(b \gt 0, b\neq 1)$の値の範囲について考える。
④を満たすbの値の範囲は$a \gt 1$のときは$\boxed{\ \ チ\ \ }$であり、
$0 \lt a \lt 1$のときは$\boxed{\ \ ツ\ \ }$である。
$\boxed{\ \ チ\ \ }$の解答群
$⓪0 \lt b \lt \frac{1}{a}, 1 \lt b \lt a ①0 \lt b \lt \frac{1}{a}, a \lt b$
$②\frac{1}{a} \lt b \lt 1, 1 \lt b \lt a ③\frac{1}{a} \lt b \lt 1, a \lt b$
$\boxed{\ \ ツ\ \ }$の解答群
$⓪0 \lt b \lt a, 1 \lt b \lt \frac{1}{a} ①0 \lt b \lt a, \frac{1}{a} \lt b$
$②a \lt b \lt 1, 1 \lt b \lt \frac{1}{a} ③a \lt b \lt 1, \frac{1}{a} \lt b$
(4)$p=\frac{12}{13}, q=\frac{12}{11}, r=\frac{14}{13}$とする。
次の⓪~③のうち、正しいものは$\boxed{\ \ テ\ \ }$である。
$\boxed{\ \ テ\ \ }$の解答群
$⓪\log_pq \gt \log_qp$かつ$\log_pr \gt \log_rp$
$①\log_pq \gt \log_qp$かつ$\log_pr \lt \log_rp$
$②\log_pq \lt \log_qp$かつ$\log_pr \gt \log_rp$
$③\log_pq \lt \log_qp$かつ$\log_pr \lt \log_rp$
2022共通テスト数学過去問
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
[2]a,bは正の実数であり、$a\neq 1,b\neq 1$を満たすとする。太郎さんは
$\log_ab$と$\log_ba$の大小関係を調べることにした。
(1)太郎さんは次のような考察をした。
まず、$\log_39=\boxed{\ \ ス\ \ }, \log_93=\frac{1}{\boxed{\ \ ス\ \ }}$である、この場合
$\log_39 \gt \log_93$
が成り立つ。
一方、$\log_{\frac{1}{4}}\boxed{\ \ セ\ \ }=-\frac{3}{2},\log_{\boxed{セ}}\frac{1}{4}=-\frac{2}{3}$である。この場合
$\log_{\frac{1}{4}}\boxed{\ \ セ\ \ } \lt \log_{\boxed{セ}}\frac{1}{4}$
が成り立つ。
(2)ここで
$\log_ab=t \ldots①$
とおく。
(1)の考察をもとにして、太郎さんは次の式が成り立つと推測し、
それが正しいことを確かめることにした。
$\log_ba=\frac{1}{t} \ldots②$
①により、$\boxed{\ \ ソ\ \ }$である。このことにより$\boxed{\ \ タ\ \ }$が得られ、②が
成り立つことが確かめられる。
$\boxed{\ \ ソ\ \ }$の解答群
$⓪a^k=t ①a^t=b ②b^a=t$
$③b^t=a ④t^a=b ⑤t^b=a$
$\boxed{\ \ タ\ \ }$の解答群
$⓪a=t^{\frac{1}{b}} ①a=b^{\frac{1}{t}} ②b=t^{\frac{1}{a}}$
$③b=a^{\frac{1}{t}} ④t=b^{\frac{1}{a}} ⑤t=a^{\frac{1}{b}}$
(3)次に、太郎さんは(2)の考察をもとにして
$t \gt \frac{1}{t} \ldots③$
を満たす実数$t(t\neq 0)$の値の範囲を求めた。
太郎さんの考察
$t \gt 0$ならば、③の両辺にtを掛けることにより、$t^2 \gt 1$を得る。
このような$t(t \gt 0)$の値の範囲は$1 \lt t$である。
$t \lt 0$ならば、③の両辺にtを掛けることにより、$t^2 \lt 1$を得る。
このような$t(t \lt 0)$の値の範囲は$-1 \lt t \lt 0$である。
この考察により、③を満たす$t(t\neq 0)$の値の範囲は
$-1 \lt t \lt 0, 1 \lt t$
であることが分かる。
ここで、aの値を一つ定めたとき、不等式
$\log_ab \gt \log_ba \ldots④$
を満たす実数$b(b \gt 0, b\neq 1)$の値の範囲について考える。
④を満たすbの値の範囲は$a \gt 1$のときは$\boxed{\ \ チ\ \ }$であり、
$0 \lt a \lt 1$のときは$\boxed{\ \ ツ\ \ }$である。
$\boxed{\ \ チ\ \ }$の解答群
$⓪0 \lt b \lt \frac{1}{a}, 1 \lt b \lt a ①0 \lt b \lt \frac{1}{a}, a \lt b$
$②\frac{1}{a} \lt b \lt 1, 1 \lt b \lt a ③\frac{1}{a} \lt b \lt 1, a \lt b$
$\boxed{\ \ ツ\ \ }$の解答群
$⓪0 \lt b \lt a, 1 \lt b \lt \frac{1}{a} ①0 \lt b \lt a, \frac{1}{a} \lt b$
$②a \lt b \lt 1, 1 \lt b \lt \frac{1}{a} ③a \lt b \lt 1, \frac{1}{a} \lt b$
(4)$p=\frac{12}{13}, q=\frac{12}{11}, r=\frac{14}{13}$とする。
次の⓪~③のうち、正しいものは$\boxed{\ \ テ\ \ }$である。
$\boxed{\ \ テ\ \ }$の解答群
$⓪\log_pq \gt \log_qp$かつ$\log_pr \gt \log_rp$
$①\log_pq \gt \log_qp$かつ$\log_pr \lt \log_rp$
$②\log_pq \lt \log_qp$かつ$\log_pr \gt \log_rp$
$③\log_pq \lt \log_qp$かつ$\log_pr \lt \log_rp$
2022共通テスト数学過去問
[2]a,bは正の実数であり、$a\neq 1,b\neq 1$を満たすとする。太郎さんは
$\log_ab$と$\log_ba$の大小関係を調べることにした。
(1)太郎さんは次のような考察をした。
まず、$\log_39=\boxed{\ \ ス\ \ }, \log_93=\frac{1}{\boxed{\ \ ス\ \ }}$である、この場合
$\log_39 \gt \log_93$
が成り立つ。
一方、$\log_{\frac{1}{4}}\boxed{\ \ セ\ \ }=-\frac{3}{2},\log_{\boxed{セ}}\frac{1}{4}=-\frac{2}{3}$である。この場合
$\log_{\frac{1}{4}}\boxed{\ \ セ\ \ } \lt \log_{\boxed{セ}}\frac{1}{4}$
が成り立つ。
(2)ここで
$\log_ab=t \ldots①$
とおく。
(1)の考察をもとにして、太郎さんは次の式が成り立つと推測し、
それが正しいことを確かめることにした。
$\log_ba=\frac{1}{t} \ldots②$
①により、$\boxed{\ \ ソ\ \ }$である。このことにより$\boxed{\ \ タ\ \ }$が得られ、②が
成り立つことが確かめられる。
$\boxed{\ \ ソ\ \ }$の解答群
$⓪a^k=t ①a^t=b ②b^a=t$
$③b^t=a ④t^a=b ⑤t^b=a$
$\boxed{\ \ タ\ \ }$の解答群
$⓪a=t^{\frac{1}{b}} ①a=b^{\frac{1}{t}} ②b=t^{\frac{1}{a}}$
$③b=a^{\frac{1}{t}} ④t=b^{\frac{1}{a}} ⑤t=a^{\frac{1}{b}}$
(3)次に、太郎さんは(2)の考察をもとにして
$t \gt \frac{1}{t} \ldots③$
を満たす実数$t(t\neq 0)$の値の範囲を求めた。
太郎さんの考察
$t \gt 0$ならば、③の両辺にtを掛けることにより、$t^2 \gt 1$を得る。
このような$t(t \gt 0)$の値の範囲は$1 \lt t$である。
$t \lt 0$ならば、③の両辺にtを掛けることにより、$t^2 \lt 1$を得る。
このような$t(t \lt 0)$の値の範囲は$-1 \lt t \lt 0$である。
この考察により、③を満たす$t(t\neq 0)$の値の範囲は
$-1 \lt t \lt 0, 1 \lt t$
であることが分かる。
ここで、aの値を一つ定めたとき、不等式
$\log_ab \gt \log_ba \ldots④$
を満たす実数$b(b \gt 0, b\neq 1)$の値の範囲について考える。
④を満たすbの値の範囲は$a \gt 1$のときは$\boxed{\ \ チ\ \ }$であり、
$0 \lt a \lt 1$のときは$\boxed{\ \ ツ\ \ }$である。
$\boxed{\ \ チ\ \ }$の解答群
$⓪0 \lt b \lt \frac{1}{a}, 1 \lt b \lt a ①0 \lt b \lt \frac{1}{a}, a \lt b$
$②\frac{1}{a} \lt b \lt 1, 1 \lt b \lt a ③\frac{1}{a} \lt b \lt 1, a \lt b$
$\boxed{\ \ ツ\ \ }$の解答群
$⓪0 \lt b \lt a, 1 \lt b \lt \frac{1}{a} ①0 \lt b \lt a, \frac{1}{a} \lt b$
$②a \lt b \lt 1, 1 \lt b \lt \frac{1}{a} ③a \lt b \lt 1, \frac{1}{a} \lt b$
(4)$p=\frac{12}{13}, q=\frac{12}{11}, r=\frac{14}{13}$とする。
次の⓪~③のうち、正しいものは$\boxed{\ \ テ\ \ }$である。
$\boxed{\ \ テ\ \ }$の解答群
$⓪\log_pq \gt \log_qp$かつ$\log_pr \gt \log_rp$
$①\log_pq \gt \log_qp$かつ$\log_pr \lt \log_rp$
$②\log_pq \lt \log_qp$かつ$\log_pr \gt \log_rp$
$③\log_pq \lt \log_qp$かつ$\log_pr \lt \log_rp$
2022共通テスト数学過去問
投稿日:2022.01.20