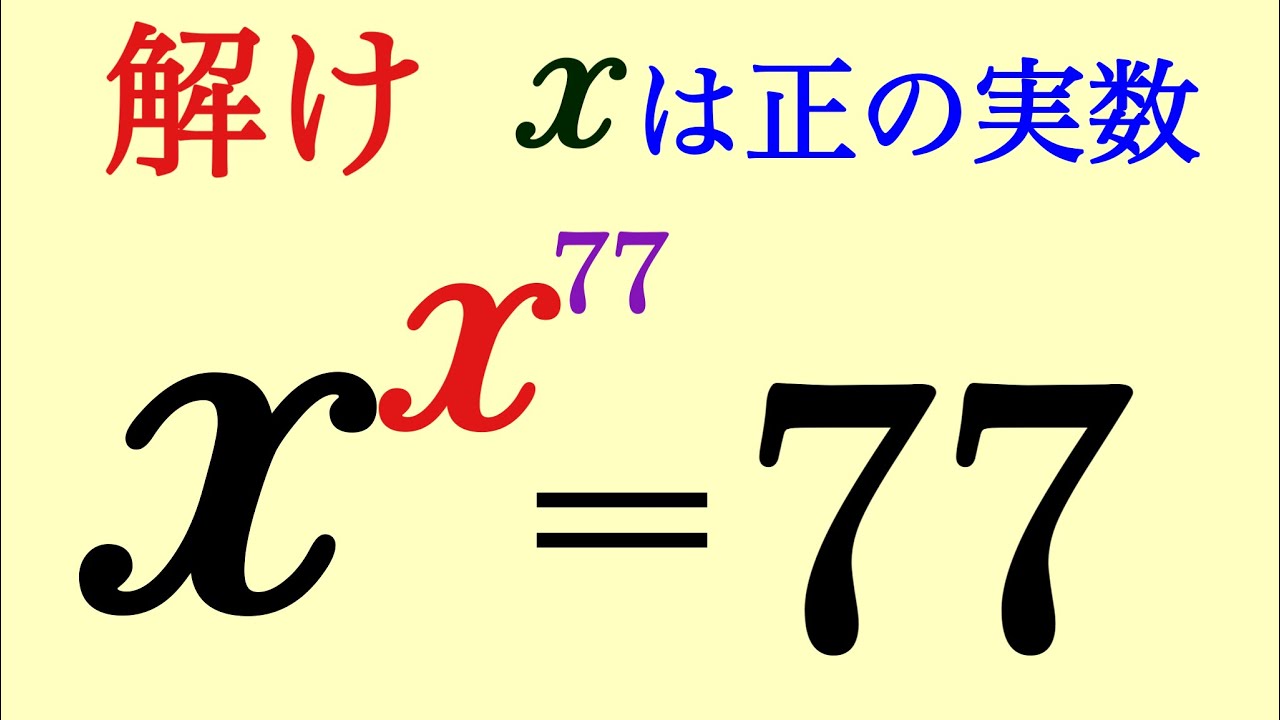問題文全文(内容文):
(1)実数$x$が$-1<x<1,x \neq 0$を満たすとき,次の不等式を示せ。
$(1-x)^{1-\dfrac{1}{x}}<(1+x)^{\dfrac{1}{x}}$
(2)次の不等式を示せ。
$0.9999^{101}<0.99<0.9999^{100}$
東大過去問
(1)実数$x$が$-1<x<1,x \neq 0$を満たすとき,次の不等式を示せ。
$(1-x)^{1-\dfrac{1}{x}}<(1+x)^{\dfrac{1}{x}}$
(2)次の不等式を示せ。
$0.9999^{101}<0.99<0.9999^{100}$
東大過去問
単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(1)実数$x$が$-1<x<1,x \neq 0$を満たすとき,次の不等式を示せ。
$(1-x)^{1-\dfrac{1}{x}}<(1+x)^{\dfrac{1}{x}}$
(2)次の不等式を示せ。
$0.9999^{101}<0.99<0.9999^{100}$
東大過去問
(1)実数$x$が$-1<x<1,x \neq 0$を満たすとき,次の不等式を示せ。
$(1-x)^{1-\dfrac{1}{x}}<(1+x)^{\dfrac{1}{x}}$
(2)次の不等式を示せ。
$0.9999^{101}<0.99<0.9999^{100}$
東大過去問
投稿日:2022.11.30