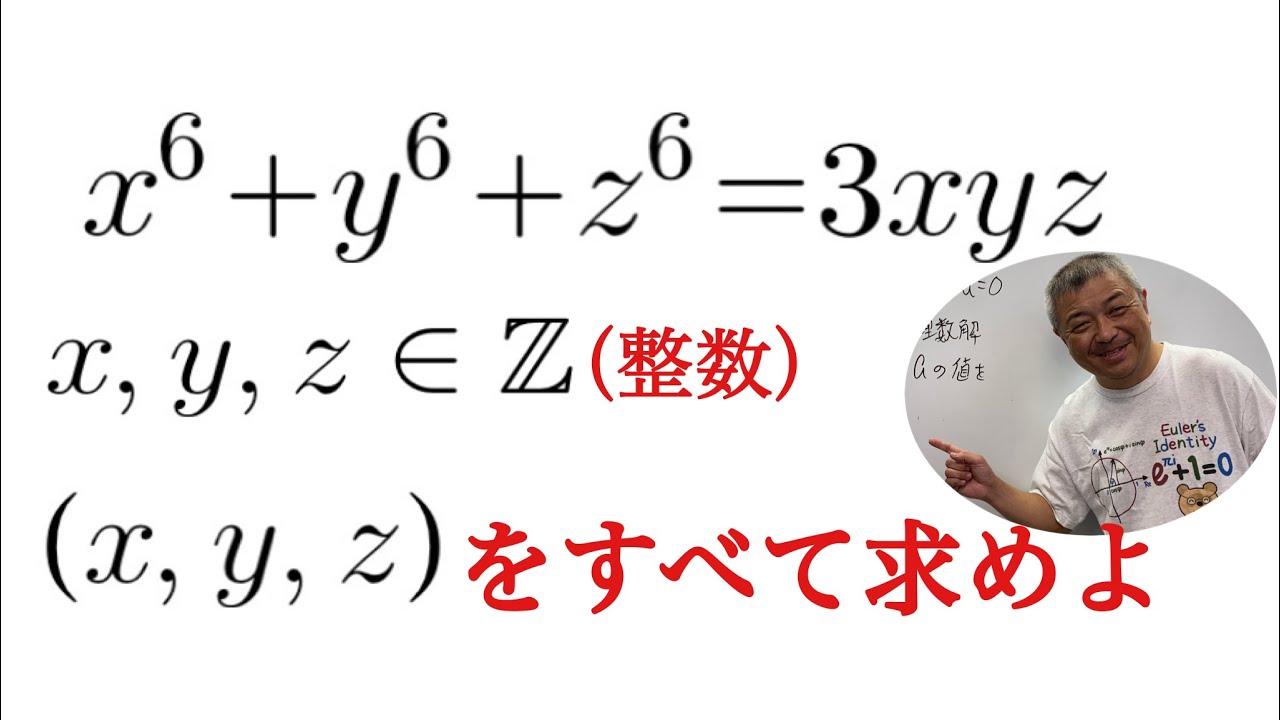奈良教育大あまりの問題 - 質問解決D.B.（データベース）

問題文全文(内容文)：
2023奈良大学過去問題
7で割ったら3余り、17で割ったら8余る自然数3桁で最大は？

単元： #整数の性質#奈良教育大学

指導講師：鈴木貫太郎

問題文全文(内容文)：
2023奈良大学過去問題
7で割ったら3余り、17で割ったら8余る自然数3桁で最大は？

投稿日：2023.10.04

単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)

指導講師：【ゼロから理解できる】高校数学・物理

問題文全文(内容文)：
方程式$xy-3x+y+2=0$を満たす整数の組$(x,y)$を全て求めよ。

この動画を見る　

単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$ 7^{n+1}$が19で割り切れるならnは平方数でないことを示せ.

この動画を見る　

単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
m,nは自然数
$4m^2+n^2 = 200 $を満たすmnの値を全て求めよ。

桃山学院高等学校

この動画を見る　

単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
ピタゴラス数,三平方の定理,整数解の求め方,質問への回答に関して解説していきます.

この動画を見る　

単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
整数(x,y,z)の組をすべて求めよ.
$x^6+y^6+z^6=3xyz$

この動画を見る　