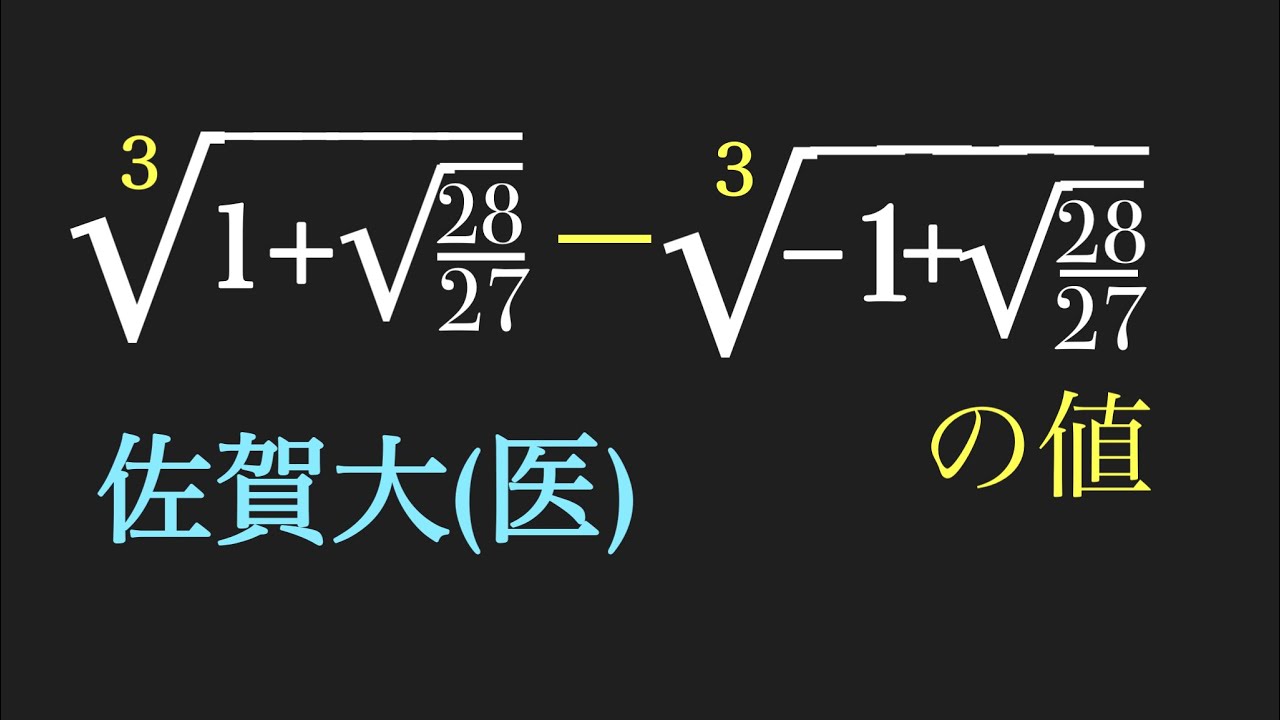2次方程式の因数分解や解の公式が不要な新しい解き方の証明

問題文全文(内容文)：
2次方程式の因数分解や解の公式が不要な新しい解き方の証明

チャプター：

00:00 はじまり

01:02 証明開始

07:02 まとめ

07:41 まとめノート

単元： #数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
2次方程式の因数分解や解の公式が不要な新しい解き方の証明

投稿日：2022.05.13

単元： #数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
x(y+z)=5 \\
y(z+x)=56 \\
z(x+y)=57 \\
\end{array}
\right.
\end{eqnarray}$

これを解け.

この動画を見る　

単元： #数Ⅱ#複素数と方程式#三角関数#剰余の定理・因数定理・組み立て除法と高次方程式#三角関数とグラフ#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：
数学$\textrm{II}$　三角関数(7)　三角方程式
$0 \leqq x \leqq 2\pi,　0 \leqq y \leqq 2\pi$において
$\cos y=\sin2x$　のグラフを描け。

この動画を見る　

単元： #数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)

指導講師：ますただ

問題文全文(内容文)：
6⃣$x^3+kx^2+2x+10=0$の解がx=-2、α、βのとき、$α^2+β^2$の値を求めよ。

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
09年　東京理科大学
$x^3-2x^2+x+5=0$の3つの解を$a,b,c$とする。次の値を求めよ。

(1)$a^3+b^3+c^3$

(2)$a^4+b^4+c^4$

この動画を見る　

単元： #剰余の定理・因数定理・組み立て除法と高次方程式

指導講師：鈴木貫太郎

問題文全文(内容文)：
解け
$(6x-1)(3x-1)(2x-1)(x-1)+x^{2}-25 = 0$

この動画を見る　