 解と判別式・解と係数の関係
解と判別式・解と係数の関係
 解と判別式・解と係数の関係
解と判別式・解と係数の関係
答えの数値で安心する問題 聖マリアンナ医科大

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#聖マリアンナ医科大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3+\sqrt[3]{4}X+4=0$
の3つの解をα,β,γとする
$(10\sqrt[3]{2}-α)(10\sqrt[3]{2}-β)(10\sqrt[3]{2}-γ)$
の値を求めよ。
この動画を見る
$x^3+\sqrt[3]{4}X+4=0$
の3つの解をα,β,γとする
$(10\sqrt[3]{2}-α)(10\sqrt[3]{2}-β)(10\sqrt[3]{2}-γ)$
の値を求めよ。
高校数学:数学検定準1級2次:問題6 3次方程式の解と係数の関係

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#数学検定#数学検定準1級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の2つの3次方程式
x³+10x²+ax+14=0
x³+2x²+bx-2=0
はそれぞれ異なる3個の解をもちますが、そのうちの2個は共通な解です。このと き、定数a,bの値および共通な2個の解を求めなさい。
この動画を見る
次の2つの3次方程式
x³+10x²+ax+14=0
x³+2x²+bx-2=0
はそれぞれ異なる3個の解をもちますが、そのうちの2個は共通な解です。このと き、定数a,bの値および共通な2個の解を求めなさい。
【数学】体系問題集 数学3 数式・関数編 111 実数解が存在することの証明

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#体系数学#体系数学問題集3(数式・関数編)
指導講師:
理数個別チャンネル
問題文全文(内容文):
a,b,cは実数の定数で、a≠0とする。2次方程式ax²+bx+c=0が、次の各場合に必ず実数解をもつことを証明せよ。
(1)$b=\frac{a}{2}+2c$
(2)$a+c=0$
(3)aとcが異符号
この動画を見る
a,b,cは実数の定数で、a≠0とする。2次方程式ax²+bx+c=0が、次の各場合に必ず実数解をもつことを証明せよ。
(1)$b=\frac{a}{2}+2c$
(2)$a+c=0$
(3)aとcが異符号
【数学】体系問題集 数学3 数式・関数編 109 虚数を含む2次方程式の解法
単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#体系数学#体系数学問題集3(数式・関数編)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の等式を満たす実数xの値を求めよ。
(1)(2+i)x²-(1+6i)x-2(3-4i)=0
(2)(3+2i)x²+(8+5i)x-3(1+i)=0
この動画を見る
次の等式を満たす実数xの値を求めよ。
(1)(2+i)x²-(1+6i)x-2(3-4i)=0
(2)(3+2i)x²+(8+5i)x-3(1+i)=0
福田のおもしろ数学036〜君は対称式を理解しているか?〜対称式の値を求める

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x+y+z=0$
$x^3+y^3+z^3=3$
$x^5+y^5+z^5=15$
のとき、$x^2+y^2+z^2$の値は??
この動画を見る
$x+y+z=0$
$x^3+y^3+z^3=3$
$x^5+y^5+z^5=15$
のとき、$x^2+y^2+z^2$の値は??
複素数と方程式 4STEP数Ⅱ 96,97 2次方程式の解と判別式2【ホーン・フィールドがていねいに解説】

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式
指導講師:
理数個別チャンネル
問題文全文(内容文):
(4STEP問題94)
2つの2次方程式x²+mx+m=0, x²+mx+1=0がともに虚数解をもつとき、定数mの値の範囲を定めよ。
(4STEP問題95)
2つの2次方程式x²+2mx-2m=0, x²+(m-1)x+m²=0が次の条件を満たすとき、定数mの値の範囲を定めよ。
(1)少なくとも一方が実数解をもつ
(2)一方だけが実数解をもつ
この動画を見る
(4STEP問題94)
2つの2次方程式x²+mx+m=0, x²+mx+1=0がともに虚数解をもつとき、定数mの値の範囲を定めよ。
(4STEP問題95)
2つの2次方程式x²+2mx-2m=0, x²+(m-1)x+m²=0が次の条件を満たすとき、定数mの値の範囲を定めよ。
(1)少なくとも一方が実数解をもつ
(2)一方だけが実数解をもつ
複素数と方程式 4STEP数Ⅱ 94,95 2次方程式の解と判別式【ホーン・フィールドがていねいに解説】

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式
指導講師:
理数個別チャンネル
問題文全文(内容文):
(4STEP問題94)
2つの2次方程式x²+mx+m=0, x²+mx+1=0がともに虚数解をもつとき、定数mの値の範囲を定めよ。
(4STEP問題95)
2つの2次方程式x²+2mx-2m=0, x²+(m-1)x+m²=0が次の条件を満たすとき、定数mの値の範囲を定めよ。
(1)少なくとも一方が実数解をもつ
(2)一方だけが実数解をもつ
この動画を見る
(4STEP問題94)
2つの2次方程式x²+mx+m=0, x²+mx+1=0がともに虚数解をもつとき、定数mの値の範囲を定めよ。
(4STEP問題95)
2つの2次方程式x²+2mx-2m=0, x²+(m-1)x+m²=0が次の条件を満たすとき、定数mの値の範囲を定めよ。
(1)少なくとも一方が実数解をもつ
(2)一方だけが実数解をもつ
4次方程式の解と係数の関係 答えがあっていればなんでもいいか!山口大

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$
\begin{eqnarray}
&&2023山口大\\
&&x^4-6x^2+25=0の4つの解をp,q,r,s\\
&&①p^3+q^3+r^3+s^3\\
&&②p^3q^3+p^3r^3+p^3s^3+q^3r^3+q^3s^3+r^3s^3
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
&&2023山口大\\
&&x^4-6x^2+25=0の4つの解をp,q,r,s\\
&&①p^3+q^3+r^3+s^3\\
&&②p^3q^3+p^3r^3+p^3s^3+q^3r^3+q^3s^3+r^3s^3
\end{eqnarray}
$
東京医科大 4次方程式

単元:
#解と判別式・解と係数の関係
指導講師:
鈴木貫太郎
問題文全文(内容文):
2021東京医科大学過去問題
$
\begin{eqnarray}
\\
&&x^4+11x^3+31x^2+11x+1=0の4つの解をα、β、γ、δとする\\
&&①\frac{1}{α}+\frac{1}{β}+\frac{1}{γ}+\frac{1}{δ}\\
&&②α^2+β^2+γ^2+δ^2\\
&&③α^3+β^3+γ^3+δ^3\\
&&①②③の値
\end{eqnarray}
$
この動画を見る
2021東京医科大学過去問題
$
\begin{eqnarray}
\\
&&x^4+11x^3+31x^2+11x+1=0の4つの解をα、β、γ、δとする\\
&&①\frac{1}{α}+\frac{1}{β}+\frac{1}{γ}+\frac{1}{δ}\\
&&②α^2+β^2+γ^2+δ^2\\
&&③α^3+β^3+γ^3+δ^3\\
&&①②③の値
\end{eqnarray}
$
千葉大 複素数の方程式

単元:
#数Ⅱ#複素数と方程式#複素数#解と判別式・解と係数の関係#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023千葉大学過去問題
①$z^3=i$を解け
②$z^{100}=i$の解で 実部$\leqq \frac{1}{2}$
かつ虚部$\geqq 0$は何個あるか?
この動画を見る
2023千葉大学過去問題
①$z^3=i$を解け
②$z^{100}=i$の解で 実部$\leqq \frac{1}{2}$
かつ虚部$\geqq 0$は何個あるか?
複素数のいい問題 山形大

単元:
#数Ⅱ#複素数と方程式#複素数#解と判別式・解と係数の関係#数学(高校生)#山形大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
山形大学過去問題
複素数平面上の相異なる3点A(α),B(β),C(γ)において
$α^2+β^2+γ^2=αβ+βγ+αγ$が成り立つなら△ABCは正三角形であることを示せ
この動画を見る
山形大学過去問題
複素数平面上の相異なる3点A(α),B(β),C(γ)において
$α^2+β^2+γ^2=αβ+βγ+αγ$が成り立つなら△ABCは正三角形であることを示せ
意外と差がつく?しっかりと取りたい問題です【大阪大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#三角関数#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
a,bを実数とする。θについての方程式$\cos 2θ=a\ sin θ+b$が実数解をもつような点(a,b)の存在範囲を座標平面上に図示せよ。
この動画を見る
a,bを実数とする。θについての方程式$\cos 2θ=a\ sin θ+b$が実数解をもつような点(a,b)の存在範囲を座標平面上に図示せよ。
4次方程式の解と係数の関係?
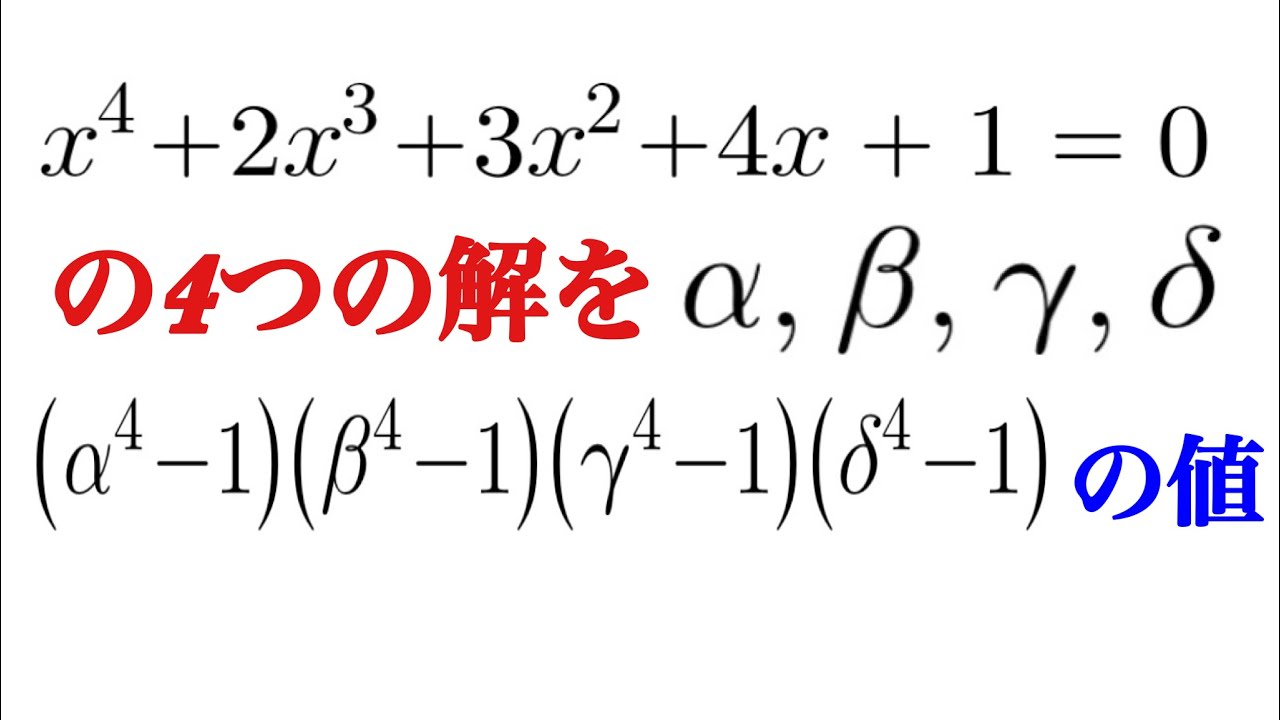
単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x⁴+2x³+3x²+4x+1=0の4つの解をα,β,γ,δとおくとき
(α⁴-1)(β⁴-1)(γ⁴-1)(δ⁴-1)の値を求めよ
この動画を見る
x⁴+2x³+3x²+4x+1=0の4つの解をα,β,γ,δとおくとき
(α⁴-1)(β⁴-1)(γ⁴-1)(δ⁴-1)の値を求めよ
【数Ⅱ】複素数と方程式:解と係数の関係:「解と係数の関係」の基本を10分でマスター!

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
解と係数の関係の基本を10分でマスター!例題も4問解説!
この動画を見る
解と係数の関係の基本を10分でマスター!例題も4問解説!
連立二元二次方程式2023
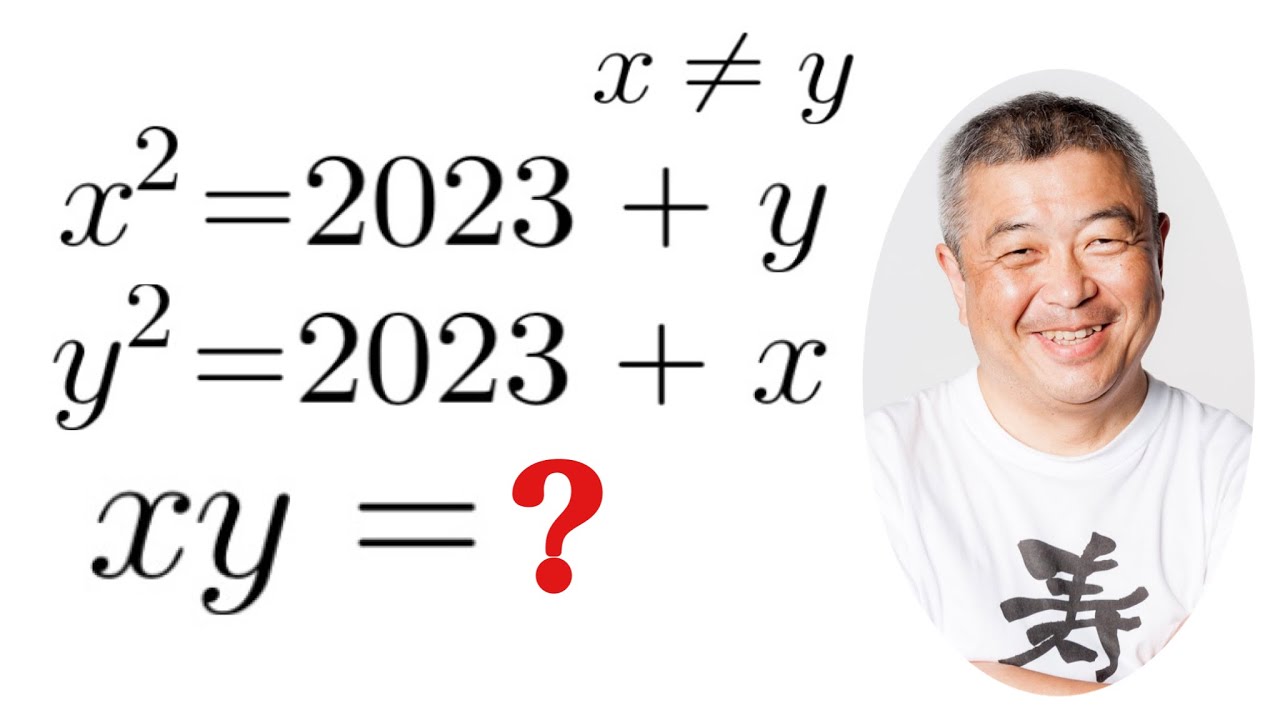
単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x²=2023+y
y²=2023+x
このときxyの値を求めよ
この動画を見る
x²=2023+y
y²=2023+x
このときxyの値を求めよ
福田の数学〜慶應義塾大学2022年看護医療学部第1問(5)〜解と係数の関係と式の値の計算

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
{\large\boxed{1}}\ (5)iを虚数単位とし、\alpha=\frac{1-\sqrt3i}{4}とする。このとき、\hspace{80pt}\\
a,bを実数とする2次方程式x^2+ax+b=0の解の1つが\alphaであるならば、\\
a=\boxed{\ \ ア\ \ },\ b=\boxed{\ \ イ\ \ }\ である。\hspace{100pt}\\
また、f(x)=4x^4-3x^3+2x^2とするとき、f(\alpha)の値は\boxed{\ \ ウ\ \ }である。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
{\large\boxed{1}}\ (5)iを虚数単位とし、\alpha=\frac{1-\sqrt3i}{4}とする。このとき、\hspace{80pt}\\
a,bを実数とする2次方程式x^2+ax+b=0の解の1つが\alphaであるならば、\\
a=\boxed{\ \ ア\ \ },\ b=\boxed{\ \ イ\ \ }\ である。\hspace{100pt}\\
また、f(x)=4x^4-3x^3+2x^2とするとき、f(\alpha)の値は\boxed{\ \ ウ\ \ }である。
\end{eqnarray}
数学オリンピック予選

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数#解と判別式・解と係数の関係#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 有理数係数の2次方程式 x^{2n}+a_1x^{2n-1}+a_2x^{2n-2}+・・・・・・+a_{2n-1}x+a_{2n}=0の解はすべてx^2+5x+7=0の解にもなっている.a_1の値を求めよ.$
この動画を見る
$ 有理数係数の2次方程式 x^{2n}+a_1x^{2n-1}+a_2x^{2n-2}+・・・・・・+a_{2n-1}x+a_{2n}=0の解はすべてx^2+5x+7=0の解にもなっている.a_1の値を求めよ.$
99999乗【数学】

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#4STEP数学Ⅱ+BのB問題解説(新課程2022年以降)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ \alpha,\beta$を$x^2-x+1=0$の異なる解とするとき、
$\alpha^{99999}+\beta^{99999}$の値を求めよ。
この動画を見る
$ \alpha,\beta$を$x^2-x+1=0$の異なる解とするとき、
$\alpha^{99999}+\beta^{99999}$の値を求めよ。
【数Ⅱ】複素数と方程式:x²+x+1=0の2解をα、βとする。(1)α+β(2)α³+β³(3)α¹⁰⁰+β¹⁰⁰の値を求めよ。

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
x²+x+1=0の2解をα,βとする。(1)α+β(2)α³+β³(3)α¹⁰⁰+β¹⁰⁰の値を求めよ。
この動画を見る
x²+x+1=0の2解をα,βとする。(1)α+β(2)α³+β³(3)α¹⁰⁰+β¹⁰⁰の値を求めよ。
【数Ⅱ】複素数と方程式:解と係数の関係(3次)の利用

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
3次方程式x³+ax²+bx+20=0の解の1つがx=3-iであるとき、実数の定数a,bの値と、他の解を求めよう。
この動画を見る
3次方程式x³+ax²+bx+20=0の解の1つがx=3-iであるとき、実数の定数a,bの値と、他の解を求めよう。
福田の数学〜慶應義塾大学2021年薬学部第1問(2)〜解の差が1の2次方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#解と判別式・解と係数の関係#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
{\Large\boxed{1}} (2)xの関数f(x)=x^2+ax+bがある。方程式f(x)=0の2つの実数解の差が\\
1であり、xの値が2から5まで変わるときのf(x)の平均変化率が\frac{13}{2}であるとき、\\
aの値は\ \boxed{\ \ イ\ \ }、bの値は\ \boxed{\ \ ウ\ \ }\ である。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
{\Large\boxed{1}} (2)xの関数f(x)=x^2+ax+bがある。方程式f(x)=0の2つの実数解の差が\\
1であり、xの値が2から5まで変わるときのf(x)の平均変化率が\frac{13}{2}であるとき、\\
aの値は\ \boxed{\ \ イ\ \ }、bの値は\ \boxed{\ \ ウ\ \ }\ である。
\end{eqnarray}
福田の1日1題わかった数学〜高校2年生第3回〜高次方程式と連立方程式

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{II} 高次方程式\\
\left\{\begin{array}{1}
a^3x+a^2y+az=1\\
b^3x+b^2y+bz=1\\
c^3x+c^2y+cz=1\\
\end{array}\right.
を解け。\\
\\
ただし、a,b,cは異なる数で0でない。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{II} 高次方程式\\
\left\{\begin{array}{1}
a^3x+a^2y+az=1\\
b^3x+b^2y+bz=1\\
c^3x+c^2y+cz=1\\
\end{array}\right.
を解け。\\
\\
ただし、a,b,cは異なる数で0でない。
\end{eqnarray}
福田の1日1題わかった数学〜高校2年生第2回〜高次方程式と整数解

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{II} 高次方程式\\
3次方程式x^3-7x+n=0 が\\
3つの整数解をもつように、\\
nの値を定めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{II} 高次方程式\\
3次方程式x^3-7x+n=0 が\\
3つの整数解をもつように、\\
nの値を定めよ。
\end{eqnarray}
福田の1日1題わかった数学〜高校2年生第1回〜高次方程式

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{II} 高次方程式\\
3次方程式x^3+ax+b=0の\\
3つの解を\alpha,\beta,\gammaとし、\\
t_n=\alpha^n+\beta^n+\gamma^n\\
のとき、at_5+bt_4をa,bで表せ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{II} 高次方程式\\
3次方程式x^3+ax+b=0の\\
3つの解を\alpha,\beta,\gammaとし、\\
t_n=\alpha^n+\beta^n+\gamma^n\\
のとき、at_5+bt_4をa,bで表せ。
\end{eqnarray}
【数Ⅱ】複素数と方程式:2x²-6x-3=0の解がα、βのとき、①β²/α+α²/β②(2α²-6α-5)(2β²-6β-1)の値を求めよ。

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2x²-6x-3=0の解がα,βのとき、
①β²/α+α²/β②(2α²-6α-5)(2β²-6β-1)の値を求めよ。
この動画を見る
2x²-6x-3=0の解がα,βのとき、
①β²/α+α²/β②(2α²-6α-5)(2β²-6β-1)の値を求めよ。
【数Ⅱ】複素数と方程式:3次方程式x³-x²+2x-3=0の3つの解をα,β,γとするとき、次の式の値を求めよう。

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
3次方程式x³-x²+2x-3=0の3つの解をα,β,γとするとき、次の式の値を求めよう。
(1)α²+β²+γ²
(2)α³+β³+γ³
(3)(1/α)+(1/β)+(1/γ)
(4)(1-α)(1-β)(1-γ)
この動画を見る
3次方程式x³-x²+2x-3=0の3つの解をα,β,γとするとき、次の式の値を求めよう。
(1)α²+β²+γ²
(2)α³+β³+γ³
(3)(1/α)+(1/β)+(1/γ)
(4)(1-α)(1-β)(1-γ)
【数Ⅱ】複素数と方程式:3次方程式が異なる3つの解を持つ条件:方程式x³+(a-1)x-a=0が異なる3つの実数解をもつとき、定数aの値の範囲を求めよ。

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#ニュースコープ#ニュースコープ数学Ⅱ・B#その他(中高教材)
指導講師:
理数個別チャンネル
問題文全文(内容文):
方程式x³+(a-1)x-a=0が異なる3つの実数解をもつとき、定数aの値の範囲を求めよ。
この動画を見る
方程式x³+(a-1)x-a=0が異なる3つの実数解をもつとき、定数aの値の範囲を求めよ。
【数Ⅱ】複素数と方程式:2次方程式の解の判別(最高次数の係数が文字の場合)kは定数とする。次の方程式の解の種類を判別せよ。(k²-1)x²+2(k-1)+2=0

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
(k²-1)x²+2(k-1)+2=0の解の種類を判別せよ。
この動画を見る
(k²-1)x²+2(k-1)+2=0の解の種類を判別せよ。
