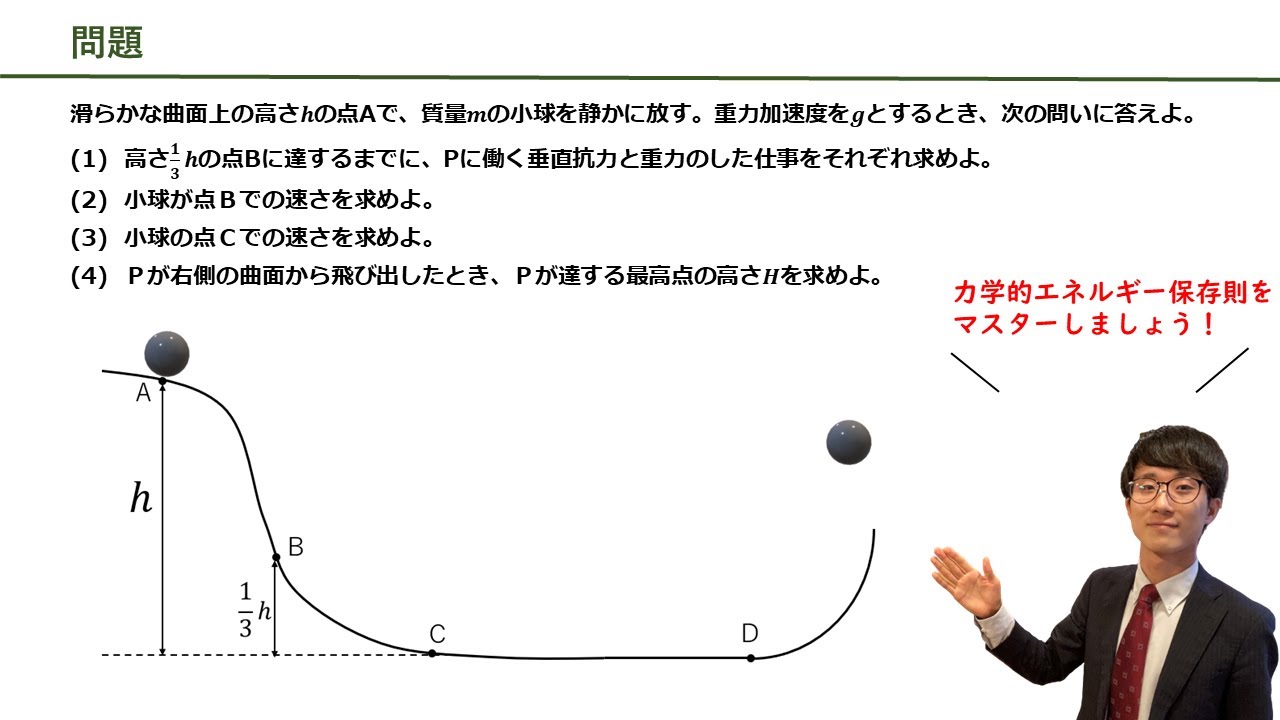
問題文全文(内容文):
(1) 図2のように小球Bが速さで左向きに跳ね返されるとき、運動量保存の法 則から
が、力学的エネルギー保存の法則から
が成立するので、m. M. Vを用いてv= ウ る。これより、小球Bが左向きに跳ね返される条件はMとmを用いて オ と表せる。さらに、小球Bが床面に落下する地点と壁の距離LBも、 m. M. V. R. gを用いてLB = カ と表せる。 $v^ prime = Box Lt$
キ V = キ のとき、小球Aは半円筒の中心○と同じ高さまで登る。つま り. V< のとき、小球Aは半円筒の中心○よりも低い高さまで登っ たのちに半円筒に沿って下ってくる。そして半円筒の端から放物線を描いて床面 に落下する。ここで、小球Aの落下地点が小球Bの落下地点と同じであると き、Mとの関係は ク と表せる。
$mv= - m * v' + lfloor mathcal J rfloor$
$1/2 * m * v ^ 2 = boxed |$
(1) 図2のように小球Bが速さで左向きに跳ね返されるとき、運動量保存の法 則から
が、力学的エネルギー保存の法則から
が成立するので、m. M. Vを用いてv= ウ る。これより、小球Bが左向きに跳ね返される条件はMとmを用いて オ と表せる。さらに、小球Bが床面に落下する地点と壁の距離LBも、 m. M. V. R. gを用いてLB = カ と表せる。 $v^ prime = Box Lt$
キ V = キ のとき、小球Aは半円筒の中心○と同じ高さまで登る。つま り. V< のとき、小球Aは半円筒の中心○よりも低い高さまで登っ たのちに半円筒に沿って下ってくる。そして半円筒の端から放物線を描いて床面 に落下する。ここで、小球Aの落下地点が小球Bの落下地点と同じであると き、Mとの関係は ク と表せる。
$mv= - m * v' + lfloor mathcal J rfloor$
$1/2 * m * v ^ 2 = boxed |$
チャプター:
00:00 オープニング
0:18 大問1
6:06 大問2
12:11 大問3
単元:
#物理#大学入試過去問(物理)#理科(高校生)#京都大学
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
(1) 図2のように小球Bが速さで左向きに跳ね返されるとき、運動量保存の法 則から
が、力学的エネルギー保存の法則から
が成立するので、m. M. Vを用いてv= ウ る。これより、小球Bが左向きに跳ね返される条件はMとmを用いて オ と表せる。さらに、小球Bが床面に落下する地点と壁の距離LBも、 m. M. V. R. gを用いてLB = カ と表せる。 $v^ prime = Box Lt$
キ V = キ のとき、小球Aは半円筒の中心○と同じ高さまで登る。つま り. V< のとき、小球Aは半円筒の中心○よりも低い高さまで登っ たのちに半円筒に沿って下ってくる。そして半円筒の端から放物線を描いて床面 に落下する。ここで、小球Aの落下地点が小球Bの落下地点と同じであると き、Mとの関係は ク と表せる。
$mv= - m * v' + lfloor mathcal J rfloor$
$1/2 * m * v ^ 2 = boxed |$
(1) 図2のように小球Bが速さで左向きに跳ね返されるとき、運動量保存の法 則から
が、力学的エネルギー保存の法則から
が成立するので、m. M. Vを用いてv= ウ る。これより、小球Bが左向きに跳ね返される条件はMとmを用いて オ と表せる。さらに、小球Bが床面に落下する地点と壁の距離LBも、 m. M. V. R. gを用いてLB = カ と表せる。 $v^ prime = Box Lt$
キ V = キ のとき、小球Aは半円筒の中心○と同じ高さまで登る。つま り. V< のとき、小球Aは半円筒の中心○よりも低い高さまで登っ たのちに半円筒に沿って下ってくる。そして半円筒の端から放物線を描いて床面 に落下する。ここで、小球Aの落下地点が小球Bの落下地点と同じであると き、Mとの関係は ク と表せる。
$mv= - m * v' + lfloor mathcal J rfloor$
$1/2 * m * v ^ 2 = boxed |$
投稿日:2024.02.08