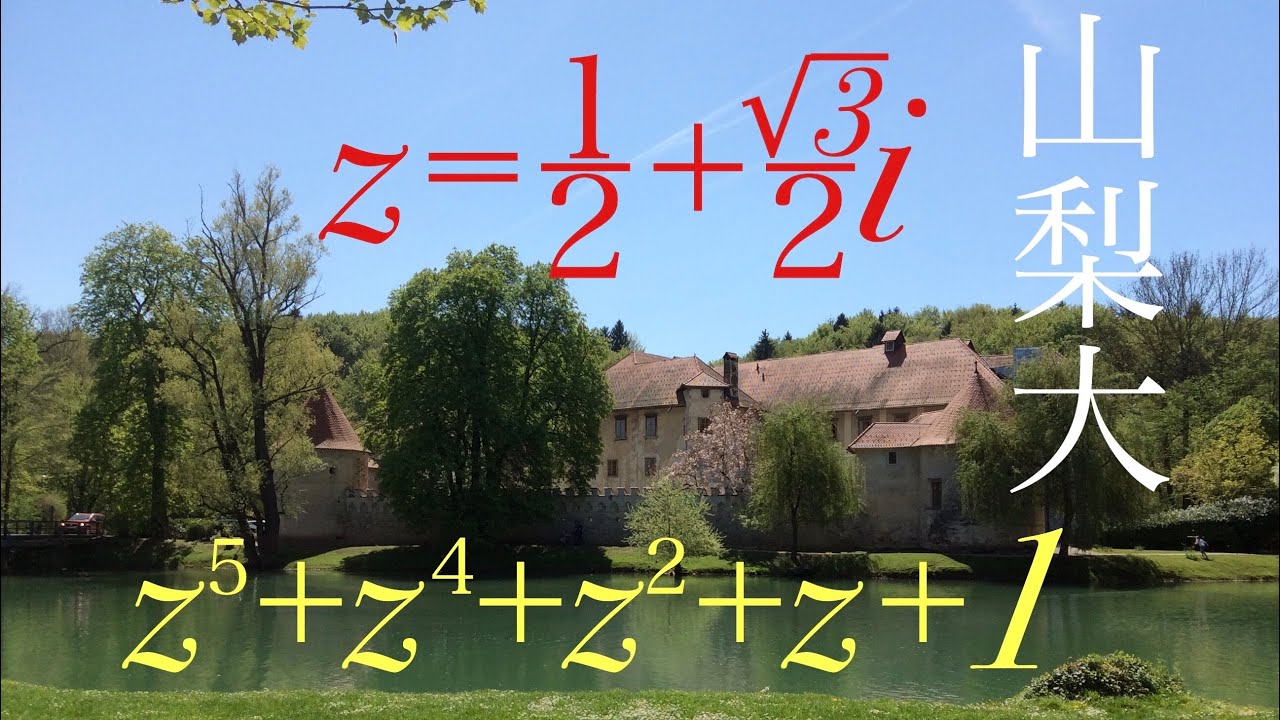問題文全文(内容文):
$w=\displaystyle \frac{-1+\sqrt{ 3 }i}{2}$
$(w+2)^n+(w^2+2)^n$が整数であることを示せ$(n$自然数$)$
出典:岡山大学 過去問
$w=\displaystyle \frac{-1+\sqrt{ 3 }i}{2}$
$(w+2)^n+(w^2+2)^n$が整数であることを示せ$(n$自然数$)$
出典:岡山大学 過去問
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#岡山大学
指導講師:
問題文全文(内容文):
$w=\displaystyle \frac{-1+\sqrt{ 3 }i}{2}$
$(w+2)^n+(w^2+2)^n$が整数であることを示せ$(n$自然数$)$
出典:岡山大学 過去問
$w=\displaystyle \frac{-1+\sqrt{ 3 }i}{2}$
$(w+2)^n+(w^2+2)^n$が整数であることを示せ$(n$自然数$)$
出典:岡山大学 過去問
投稿日:2019.11.05