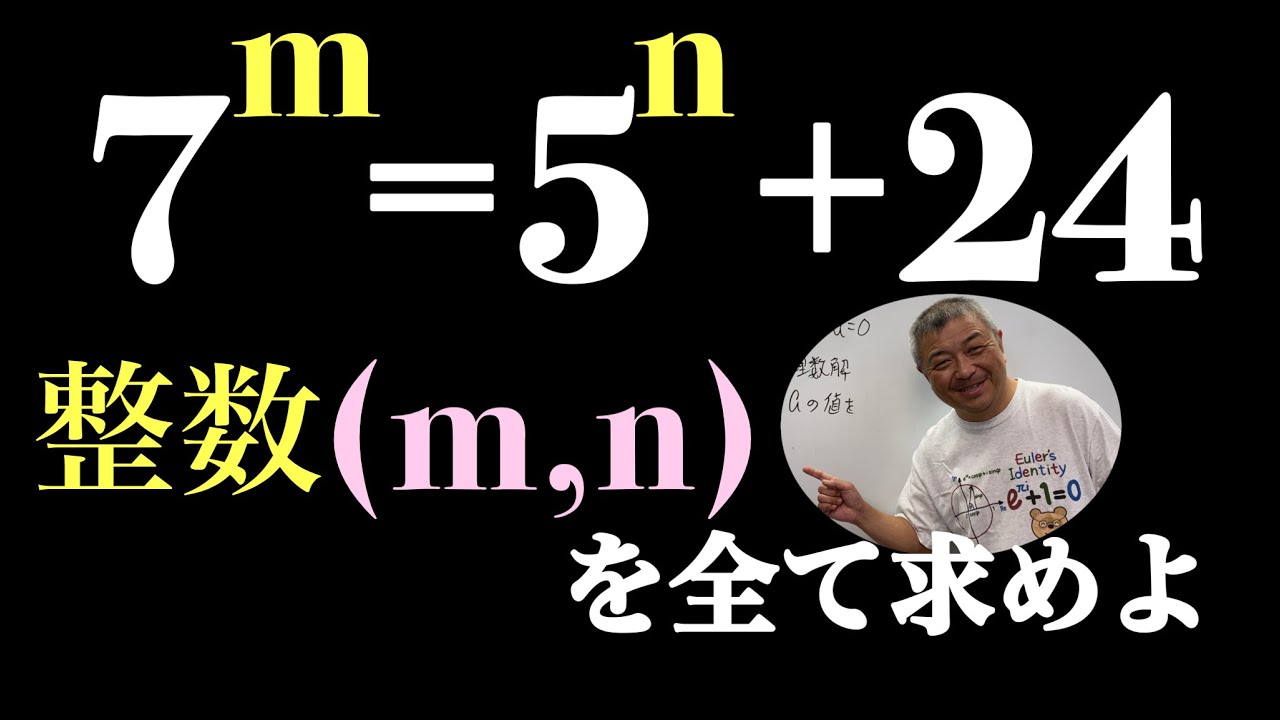問題文全文(内容文):
京都大学(理系)
2016年度(前期)第2問
p,qを素数とする。このとき$p^q+q^p$が素数となるようなp,qの値の組を全て求めよ。
京都大学(理系)
2016年度(前期)第2問
p,qを素数とする。このとき$p^q+q^p$が素数となるようなp,qの値の組を全て求めよ。
チャプター:
0:00 オープニング
0:47 問題紹介
1:18 p.qの少なくとも一方が2であることの証明
3:41 実験してみる(予想を立てる)
6:13 q≧5のときp^q+q^pが3の倍数になることの証明
単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
京都大学(理系)
2016年度(前期)第2問
p,qを素数とする。このとき$p^q+q^p$が素数となるようなp,qの値の組を全て求めよ。
京都大学(理系)
2016年度(前期)第2問
p,qを素数とする。このとき$p^q+q^p$が素数となるようなp,qの値の組を全て求めよ。
投稿日:2021.07.17