【小５ 算数】 小５－１６ 合同な図形② - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 中２数学 > 平行と合同 > 【小５　算数】　　小５－１６　　合同な図形②

【小５　算数】　　小５－１６　　合同な図形②

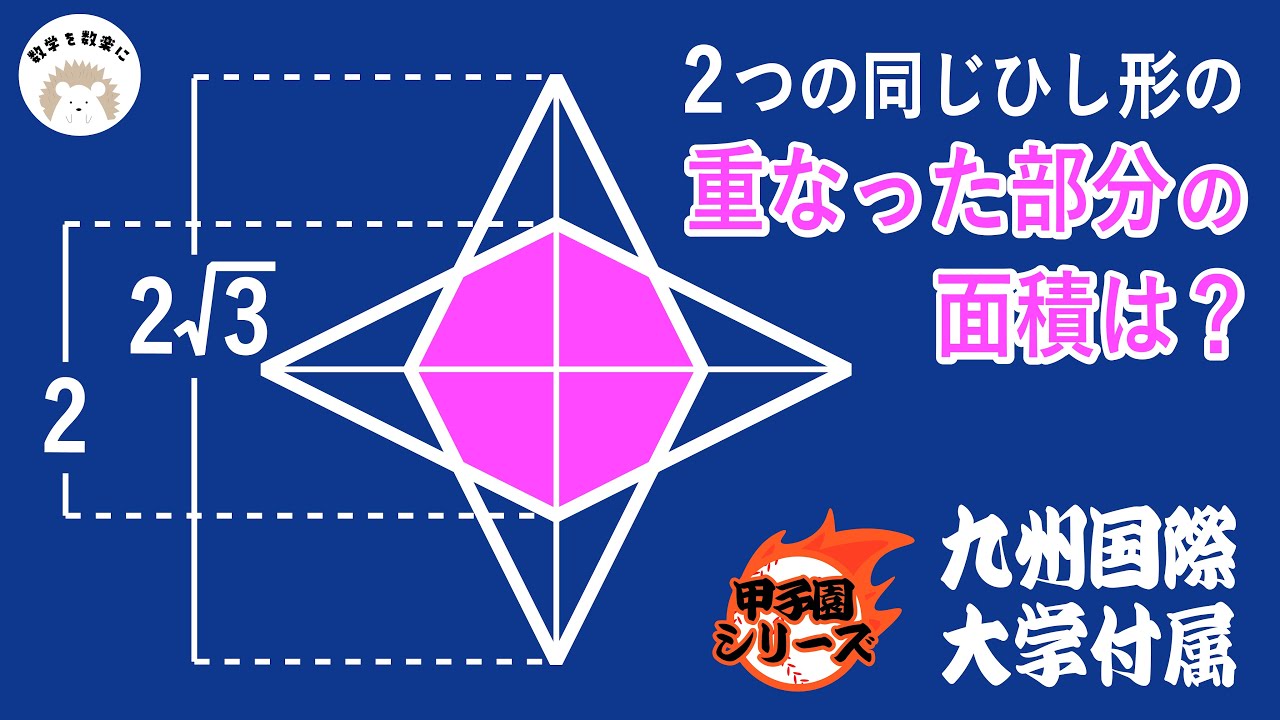
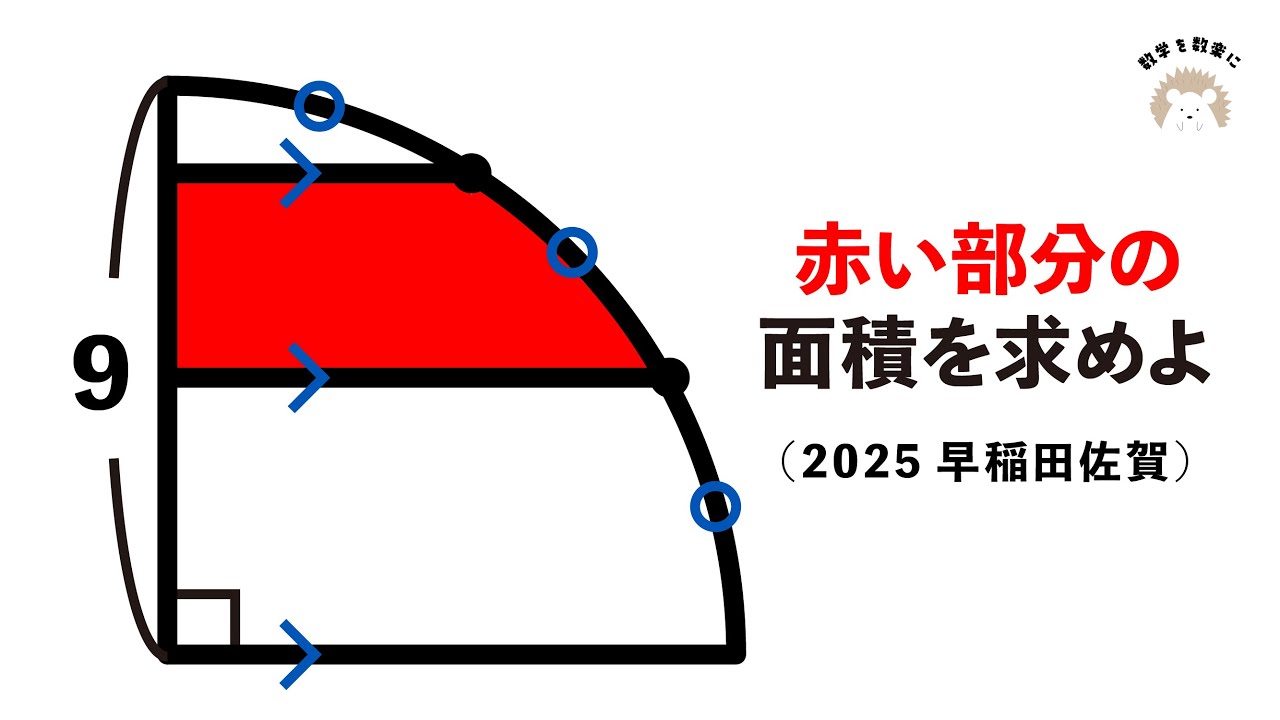
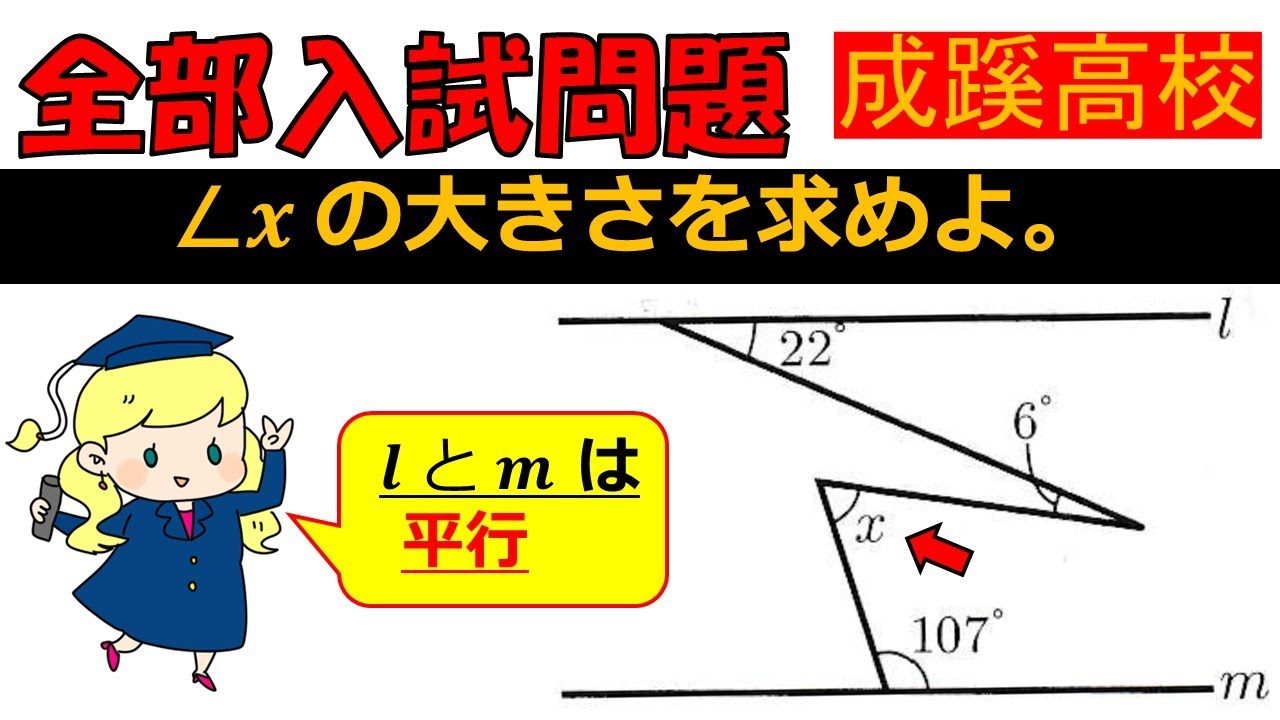
問題文全文(内容文)：
コンパスの線は①＿＿＿でね！！
コンパス→青、定規→赤
※図は動画内参照
単元： #数学(中学生)#平行と合同
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
コンパスの線は①＿＿＿でね！！
コンパス→青、定規→赤
※図は動画内参照
投稿日：2013.05.09

＜関連動画＞

【裏技】二等分線の図形を一撃で解く

アイキャッチ画像
単元： #数学(中学生)#中２数学#平行と合同
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
二等分線の図形を一撃で解く裏技紹介動画です
この動画を見る　

【受験対策】　数学－図形⑥

アイキャッチ画像
単元： #数学(中学生)#中２数学#中３数学#平行と合同#円
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
①右の図で、四角形ABCDは、AB=7cm、BC=4cmの長方形です。
この長方形を辺ABを軸として1回転させてできる立体の表面積を 求めよう。
ただし、円周率をπとする。

② 右の図のように、正五角形ABCDEの頂点、B、Dを通る直線をそれぞれℓ,mとする。ℓ//mであるとき、∠xの大きさを求めよう。

③右の図は、立方体の展開図である。
この展開図を組み立てて立方体をつくるとき、面アと垂直になる面を、 面イ～カからすべて選ぼう。

※図は動画内参照
この動画を見る　

【受験対策】数学－証明３

アイキャッチ画像
単元： #数学(中学生)#中１数学#中２数学#平行と合同#平面図形
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
右図のように,$\triangle ABC$の辺$BC$上に点$D$がある.
3点$A,B,D$を通る円と,辺$AC$との交点を$E$とするとき,
次の各問いに答えなさい.

①$\angle AEB=47°$のとき,$\angle ADC$の大きさを求めなさい.

②$AE=BD$のとき,$\triangle ACD\equiv \triangle BCE$を証明しなさい.

図は動画内参照
この動画を見る　

【中学数学】三角形と比～分かりやすく丁寧に証明～ 5-3【中３数学】

アイキャッチ画像
単元： #数学(中学生)#中２数学#平行と合同
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
DE//BCならば
AD:AB=AE:AC=DE:BC
AD:DB=AE:EC
を証明します
この動画を見る　

【数学】中2-47 対頂角 同位角 錯角③ 応用編

アイキャッチ画像
単元： #中２数学#平行と合同#三角形と四角形
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
◎ℓ//mのとき、$\angle x,\angle y $の大きさを求めよう！

①
②長方形ABCDを図のように折った。
③
※図は動画内参照
この動画を見る　
PAGE TOP