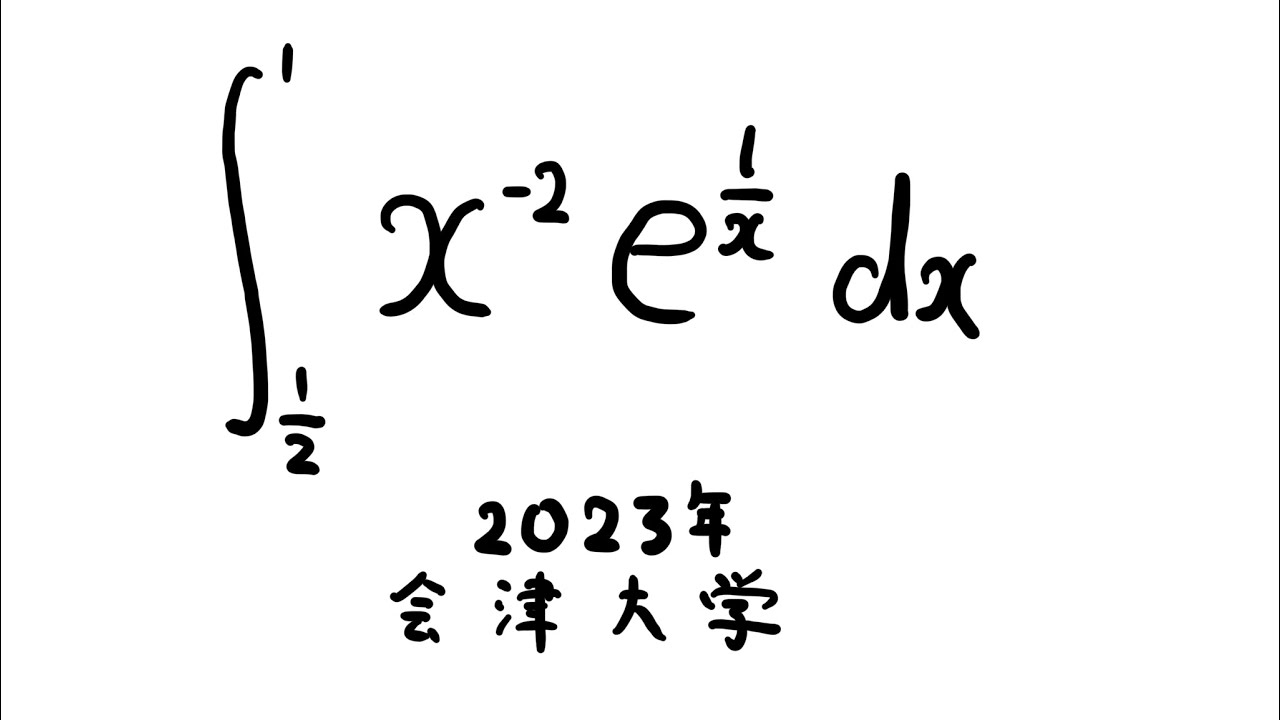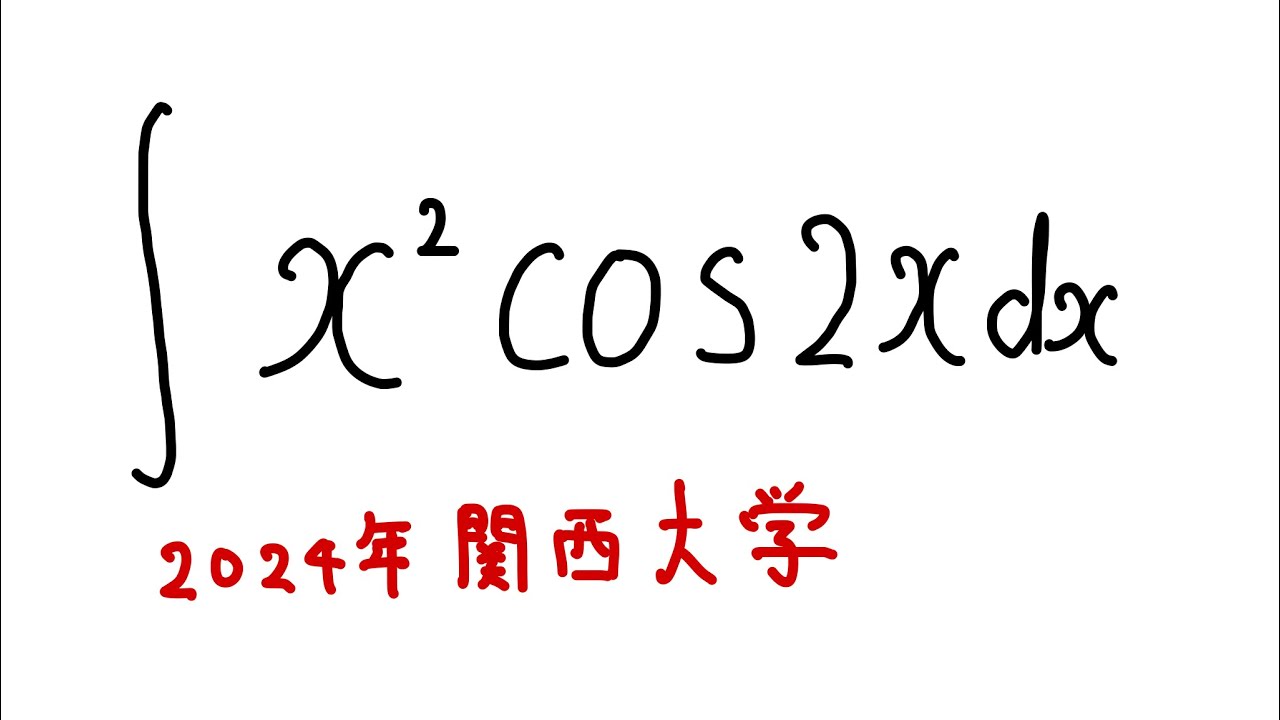なぜ定積分で面積が求められるのか？ #Shorts #毎日積分 #高校数学

問題文全文(内容文)：
なぜ定積分で面積が求められるのか？解説していきます.

単元： #数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)

指導講師：理数個別チャンネル

問題文全文(内容文)：
なぜ定積分で面積が求められるのか？解説していきます.

投稿日：2024.01.22

単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#富山大学

指導講師：鈴木貫太郎

問題文全文(内容文)：
富山大学過去問題
$y=x^2-2x+1$と$y=mx+2$とで囲まれる面積の最小値

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#弘前大学

指導講師：ますただ

問題文全文(内容文)：
$\displaystyle \int_{1}^{2} \dfrac{dx}{3+2x-x^2}$を解け.

2023弘前大学過去問題

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#中央大学#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：
${\Large\boxed{1}}$(6)次の2つの等式を満たす関数f(x)を求めよ。
$f(0)=-\frac{1}{3},　f'(x)=2x+\int_0^1f(t)dt$

2021中央大学経済学部過去問

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#福島県立医科大学

指導講師：ますただ

問題文全文(内容文)：
すべての実数$x$に対して$f(x)=x+\displaystyle \int_{0}^{1} 2^{2t+x}f(t)\ dt$を満たすとき$f(0)$を求めよ

出典：2021年福島県立医科大学　入試問題

この動画を見る　

単元： #数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
$\displaystyle \int (1-\sin^3x)\cos x$ $dx$

この動画を見る　