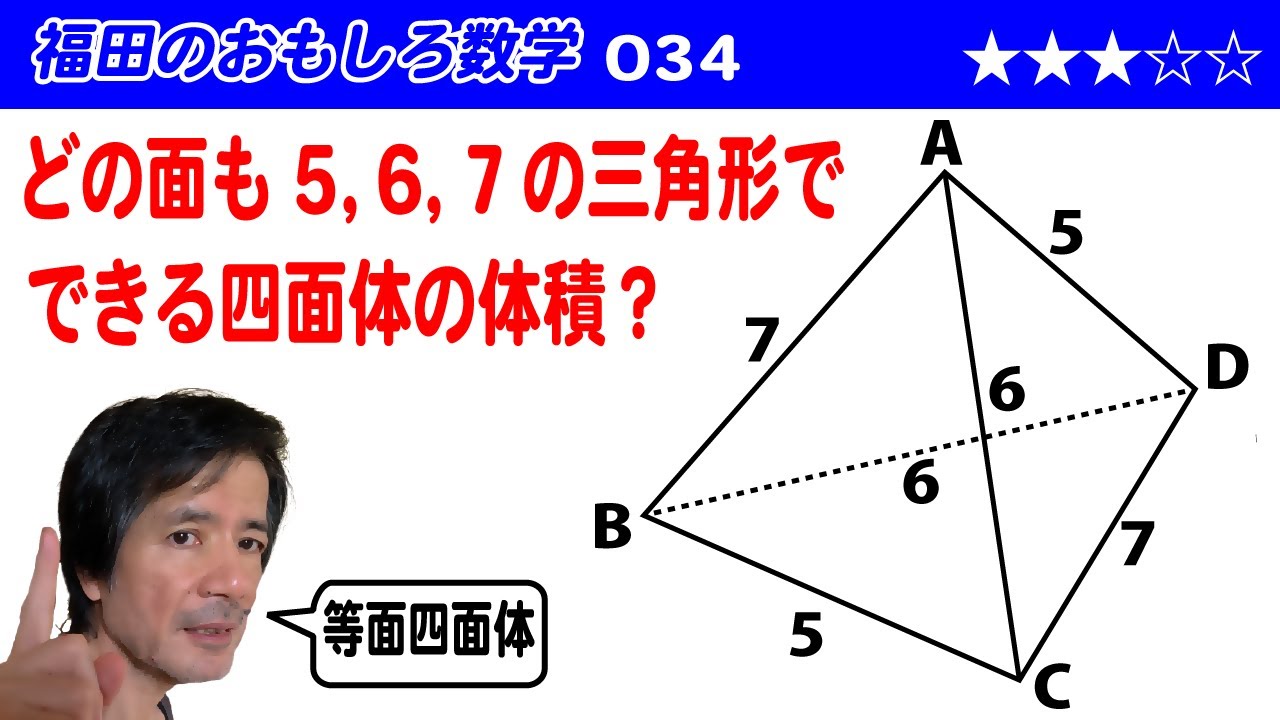
問題文全文(内容文):
右の図で曲線は$y=x^2$のグラフです。
動点Pは原点Oからと軸上を正の方向に毎秒4の速さで移動し、
動点Qは原点OからX軸上を正の方向に毎秒2の速さで移動します。
①動点P、Qが同時に出発して2秒後にできる直線PQの式は?
②①でもとめた直線PQと曲線との2つの交点において、X座標が負の点をR もう一方をSとするとき、2点R、Sの座標は?
③線分RSの長さは?
※図は動画内参照
右の図で曲線は$y=x^2$のグラフです。
動点Pは原点Oからと軸上を正の方向に毎秒4の速さで移動し、
動点Qは原点OからX軸上を正の方向に毎秒2の速さで移動します。
①動点P、Qが同時に出発して2秒後にできる直線PQの式は?
②①でもとめた直線PQと曲線との2つの交点において、X座標が負の点をR もう一方をSとするとき、2点R、Sの座標は?
③線分RSの長さは?
※図は動画内参照
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図で曲線は$y=x^2$のグラフです。
動点Pは原点Oからと軸上を正の方向に毎秒4の速さで移動し、
動点Qは原点OからX軸上を正の方向に毎秒2の速さで移動します。
①動点P、Qが同時に出発して2秒後にできる直線PQの式は?
②①でもとめた直線PQと曲線との2つの交点において、X座標が負の点をR もう一方をSとするとき、2点R、Sの座標は?
③線分RSの長さは?
※図は動画内参照
右の図で曲線は$y=x^2$のグラフです。
動点Pは原点Oからと軸上を正の方向に毎秒4の速さで移動し、
動点Qは原点OからX軸上を正の方向に毎秒2の速さで移動します。
①動点P、Qが同時に出発して2秒後にできる直線PQの式は?
②①でもとめた直線PQと曲線との2つの交点において、X座標が負の点をR もう一方をSとするとき、2点R、Sの座標は?
③線分RSの長さは?
※図は動画内参照
投稿日:2014.01.01