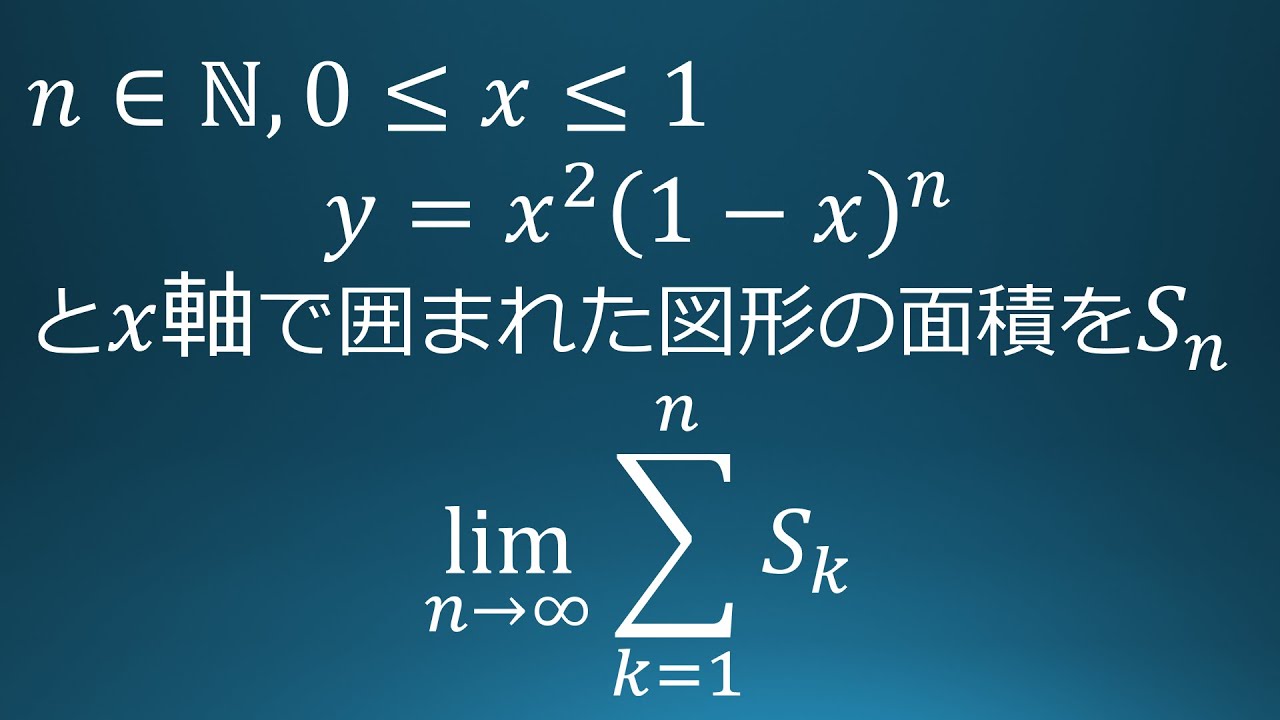http://youtu.be 問題文全文(内容文)：
$p$を$2$以上の自然数の定数とする。$n$=$2$, $3$, $4$...に対して、関数 $f_n(x) $$(n\gt0)$を
$f_n(x) = (1 + \dfrac{x}{n})(1 + \dfrac{x}{n+1}) \cdot\cdot \cdot(1 + \dfrac{x}{pn})
$
で定める。例えば$p$ = $2$のとき
$
f_2(x) = (1 + \dfrac{x}{2})(1 + \dfrac{x}{3})(1 + \dfrac{x}{4})
$
$
f_3(x) = (1 + \dfrac{x}{3})(1 + \dfrac{x}{4})(1 + \dfrac{x}{5})(1 + \dfrac{x}{6})
$
である。$f(x)=\displaystyle \lim_{ n \to \infty }f_n(x)$ $(n\gt0)$とおくとき、次の問に答えよ。
$(1)$$t$$\geqq$$0$のとき、不等式$\dfrac{t}{1+t}$$\leqq$$\log(1+t)$$\leqq$$t$ が成り立つことを示せ。ただし、対数は自然対数とする。
$(2)$ $f(x)$を求めよ。
$p$を$2$以上の自然数の定数とする。$n$=$2$, $3$, $4$...に対して、関数 $f_n(x) $$(n\gt0)$を
$f_n(x) = (1 + \dfrac{x}{n})(1 + \dfrac{x}{n+1}) \cdot\cdot \cdot(1 + \dfrac{x}{pn})
$
で定める。例えば$p$ = $2$のとき
$
f_2(x) = (1 + \dfrac{x}{2})(1 + \dfrac{x}{3})(1 + \dfrac{x}{4})
$
$
f_3(x) = (1 + \dfrac{x}{3})(1 + \dfrac{x}{4})(1 + \dfrac{x}{5})(1 + \dfrac{x}{6})
$
である。$f(x)=\displaystyle \lim_{ n \to \infty }f_n(x)$ $(n\gt0)$とおくとき、次の問に答えよ。
$(1)$$t$$\geqq$$0$のとき、不等式$\dfrac{t}{1+t}$$\leqq$$\log(1+t)$$\leqq$$t$ が成り立つことを示せ。ただし、対数は自然対数とする。
$(2)$ $f(x)$を求めよ。
単元：
#大学入試過去問(数学)#微分法と積分法#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京慈恵会医科大学#東京慈恵会医科大学
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$p$を$2$以上の自然数の定数とする。$n$=$2$, $3$, $4$...に対して、関数 $f_n(x) $$(n\gt0)$を
$f_n(x) = (1 + \dfrac{x}{n})(1 + \dfrac{x}{n+1}) \cdot\cdot \cdot(1 + \dfrac{x}{pn})
$
で定める。例えば$p$ = $2$のとき
$
f_2(x) = (1 + \dfrac{x}{2})(1 + \dfrac{x}{3})(1 + \dfrac{x}{4})
$
$
f_3(x) = (1 + \dfrac{x}{3})(1 + \dfrac{x}{4})(1 + \dfrac{x}{5})(1 + \dfrac{x}{6})
$
である。$f(x)=\displaystyle \lim_{ n \to \infty }f_n(x)$ $(n\gt0)$とおくとき、次の問に答えよ。
$(1)$$t$$\geqq$$0$のとき、不等式$\dfrac{t}{1+t}$$\leqq$$\log(1+t)$$\leqq$$t$ が成り立つことを示せ。ただし、対数は自然対数とする。
$(2)$ $f(x)$を求めよ。
$p$を$2$以上の自然数の定数とする。$n$=$2$, $3$, $4$...に対して、関数 $f_n(x) $$(n\gt0)$を
$f_n(x) = (1 + \dfrac{x}{n})(1 + \dfrac{x}{n+1}) \cdot\cdot \cdot(1 + \dfrac{x}{pn})
$
で定める。例えば$p$ = $2$のとき
$
f_2(x) = (1 + \dfrac{x}{2})(1 + \dfrac{x}{3})(1 + \dfrac{x}{4})
$
$
f_3(x) = (1 + \dfrac{x}{3})(1 + \dfrac{x}{4})(1 + \dfrac{x}{5})(1 + \dfrac{x}{6})
$
である。$f(x)=\displaystyle \lim_{ n \to \infty }f_n(x)$ $(n\gt0)$とおくとき、次の問に答えよ。
$(1)$$t$$\geqq$$0$のとき、不等式$\dfrac{t}{1+t}$$\leqq$$\log(1+t)$$\leqq$$t$ が成り立つことを示せ。ただし、対数は自然対数とする。
$(2)$ $f(x)$を求めよ。
投稿日：2025.01.19
