問題文全文(内容文):
①$\triangle ABC$の内心を$I$とし,
直線$AI$と辺$BC$の交点を$D$とする.
$AB=6,BC=%,CA=3$であるとき,$AI:ID$を求めよう.
②平行四辺形$ABCD$において,
辺$BC$の中点を$M$とし,
$AM$と$BD$の交点を$E$とする.
このとき,$\triangle BME$の面積と平行四辺形$ABCD$の
面積の比を求めよう.
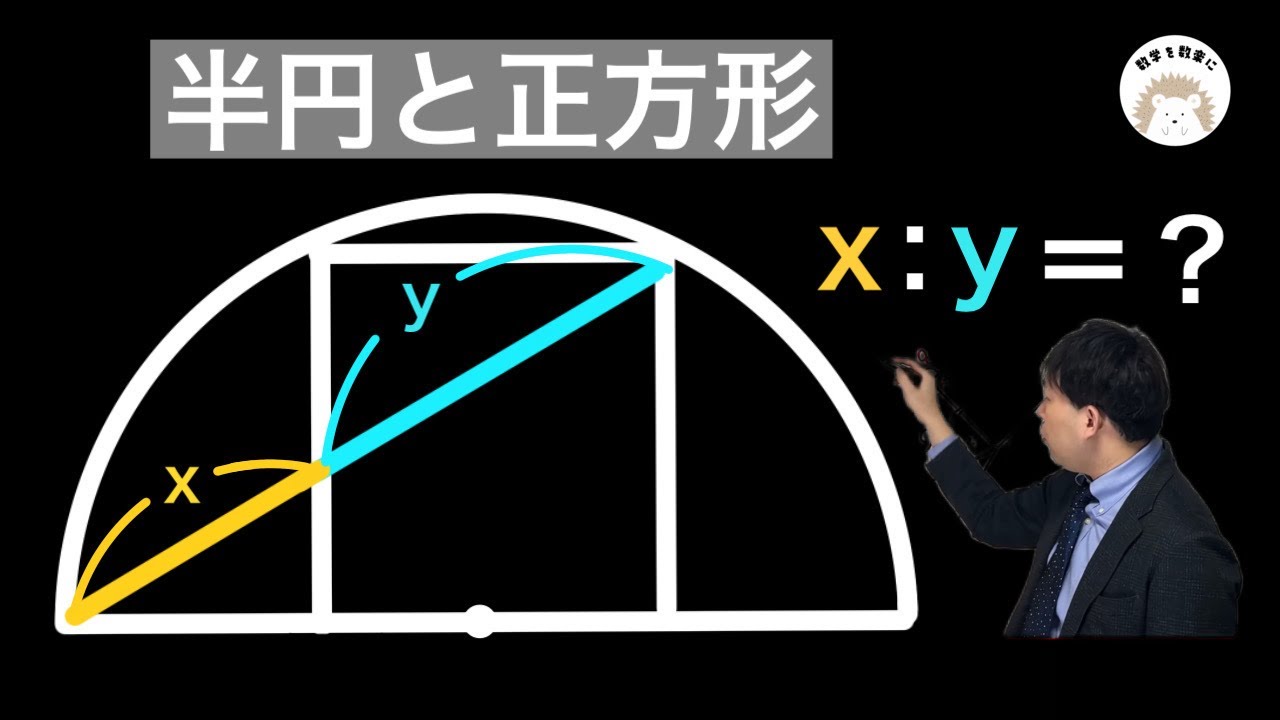
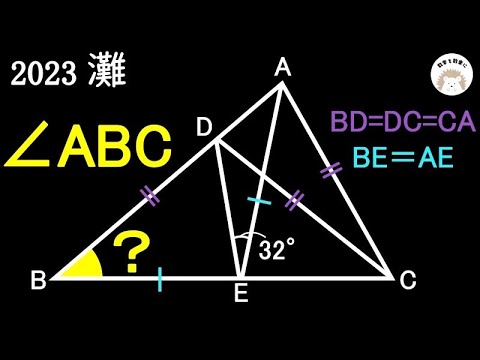
図は動画内参照
①$\triangle ABC$の内心を$I$とし,
直線$AI$と辺$BC$の交点を$D$とする.
$AB=6,BC=%,CA=3$であるとき,$AI:ID$を求めよう.
②平行四辺形$ABCD$において,
辺$BC$の中点を$M$とし,
$AM$と$BD$の交点を$E$とする.
このとき,$\triangle BME$の面積と平行四辺形$ABCD$の
面積の比を求めよう.
図は動画内参照
単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$\triangle ABC$の内心を$I$とし,
直線$AI$と辺$BC$の交点を$D$とする.
$AB=6,BC=%,CA=3$であるとき,$AI:ID$を求めよう.
②平行四辺形$ABCD$において,
辺$BC$の中点を$M$とし,
$AM$と$BD$の交点を$E$とする.
このとき,$\triangle BME$の面積と平行四辺形$ABCD$の
面積の比を求めよう.
図は動画内参照
①$\triangle ABC$の内心を$I$とし,
直線$AI$と辺$BC$の交点を$D$とする.
$AB=6,BC=%,CA=3$であるとき,$AI:ID$を求めよう.
②平行四辺形$ABCD$において,
辺$BC$の中点を$M$とし,
$AM$と$BD$の交点を$E$とする.
このとき,$\triangle BME$の面積と平行四辺形$ABCD$の
面積の比を求めよう.
図は動画内参照
投稿日:2016.04.15