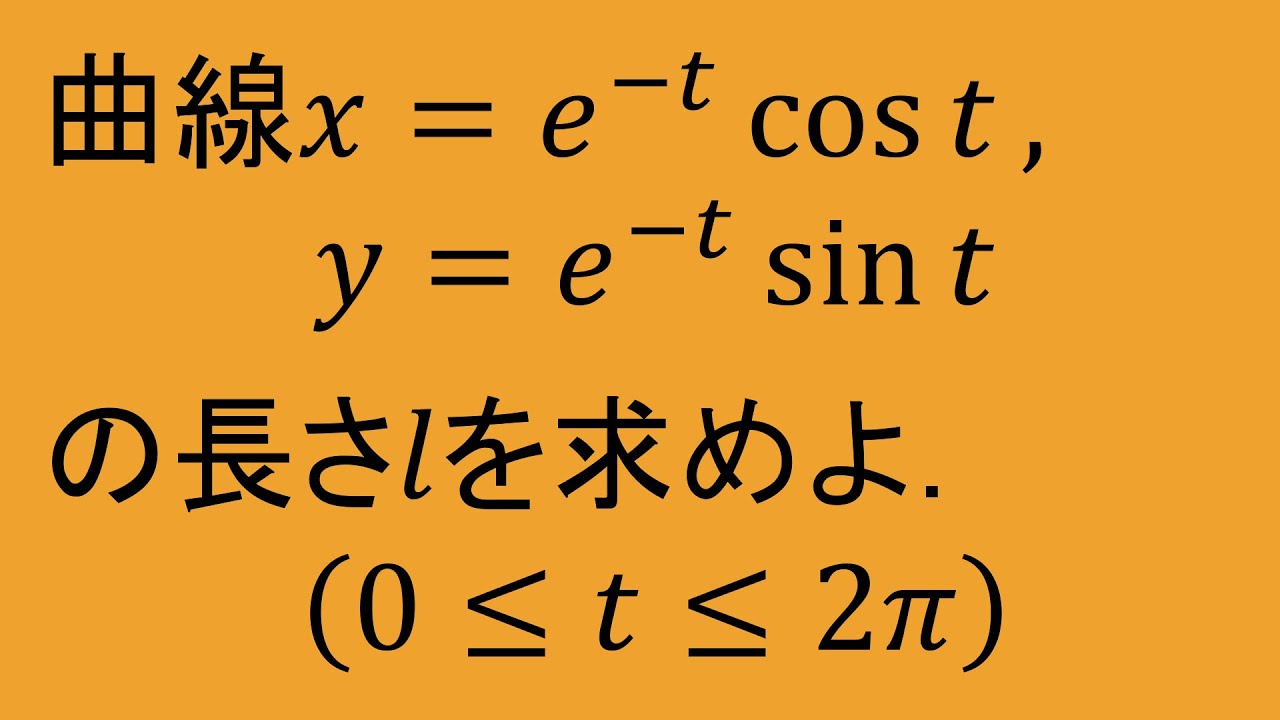問題文全文(内容文):
$\boxed{1}$
座標平面上の点
$A(0,0),B(0,1),C(1,1),D(1,0)$を考える。
実数$0\lt t \lt 1$に対して、
線分$AB,BC,CD$を$t:(1-t)$に内分する点を
それぞれ$S_t,T_t$とする。
さらに、線分$S_tT_t$を$t:(1-t)$に内分する点を
$U_t$とする。
また、点$A$を$U_0$、点$D$を$U_1$とする。
(1)点$U_t$の座標を求めよ。
(2)$t$が$0\leqq t\leqq 1$の範囲を動くときに
点$U_t$描く曲線と、
線分$AD$で囲まれた部分の面積を求めよ。
(3)$a$を$0\lt a\lt 1$を満たす実数とする。
$t$が$0\leqq t \leqq a$の範囲を動くときに点$U_t$が
描く曲線の長さを、$a$の多項式の形で求めよ。
図は動画内参照
$2025$年東京大学理系過去問題
$\boxed{1}$
座標平面上の点
$A(0,0),B(0,1),C(1,1),D(1,0)$を考える。
実数$0\lt t \lt 1$に対して、
線分$AB,BC,CD$を$t:(1-t)$に内分する点を
それぞれ$S_t,T_t$とする。
さらに、線分$S_tT_t$を$t:(1-t)$に内分する点を
$U_t$とする。
また、点$A$を$U_0$、点$D$を$U_1$とする。
(1)点$U_t$の座標を求めよ。
(2)$t$が$0\leqq t\leqq 1$の範囲を動くときに
点$U_t$描く曲線と、
線分$AD$で囲まれた部分の面積を求めよ。
(3)$a$を$0\lt a\lt 1$を満たす実数とする。
$t$が$0\leqq t \leqq a$の範囲を動くときに点$U_t$が
描く曲線の長さを、$a$の多項式の形で求めよ。
図は動画内参照
$2025$年東京大学理系過去問題
単元:
#大学入試過去問(数学)#平面上の曲線#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#東京大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
座標平面上の点
$A(0,0),B(0,1),C(1,1),D(1,0)$を考える。
実数$0\lt t \lt 1$に対して、
線分$AB,BC,CD$を$t:(1-t)$に内分する点を
それぞれ$S_t,T_t$とする。
さらに、線分$S_tT_t$を$t:(1-t)$に内分する点を
$U_t$とする。
また、点$A$を$U_0$、点$D$を$U_1$とする。
(1)点$U_t$の座標を求めよ。
(2)$t$が$0\leqq t\leqq 1$の範囲を動くときに
点$U_t$描く曲線と、
線分$AD$で囲まれた部分の面積を求めよ。
(3)$a$を$0\lt a\lt 1$を満たす実数とする。
$t$が$0\leqq t \leqq a$の範囲を動くときに点$U_t$が
描く曲線の長さを、$a$の多項式の形で求めよ。
図は動画内参照
$2025$年東京大学理系過去問題
$\boxed{1}$
座標平面上の点
$A(0,0),B(0,1),C(1,1),D(1,0)$を考える。
実数$0\lt t \lt 1$に対して、
線分$AB,BC,CD$を$t:(1-t)$に内分する点を
それぞれ$S_t,T_t$とする。
さらに、線分$S_tT_t$を$t:(1-t)$に内分する点を
$U_t$とする。
また、点$A$を$U_0$、点$D$を$U_1$とする。
(1)点$U_t$の座標を求めよ。
(2)$t$が$0\leqq t\leqq 1$の範囲を動くときに
点$U_t$描く曲線と、
線分$AD$で囲まれた部分の面積を求めよ。
(3)$a$を$0\lt a\lt 1$を満たす実数とする。
$t$が$0\leqq t \leqq a$の範囲を動くときに点$U_t$が
描く曲線の長さを、$a$の多項式の形で求めよ。
図は動画内参照
$2025$年東京大学理系過去問題
投稿日:2025.02.25