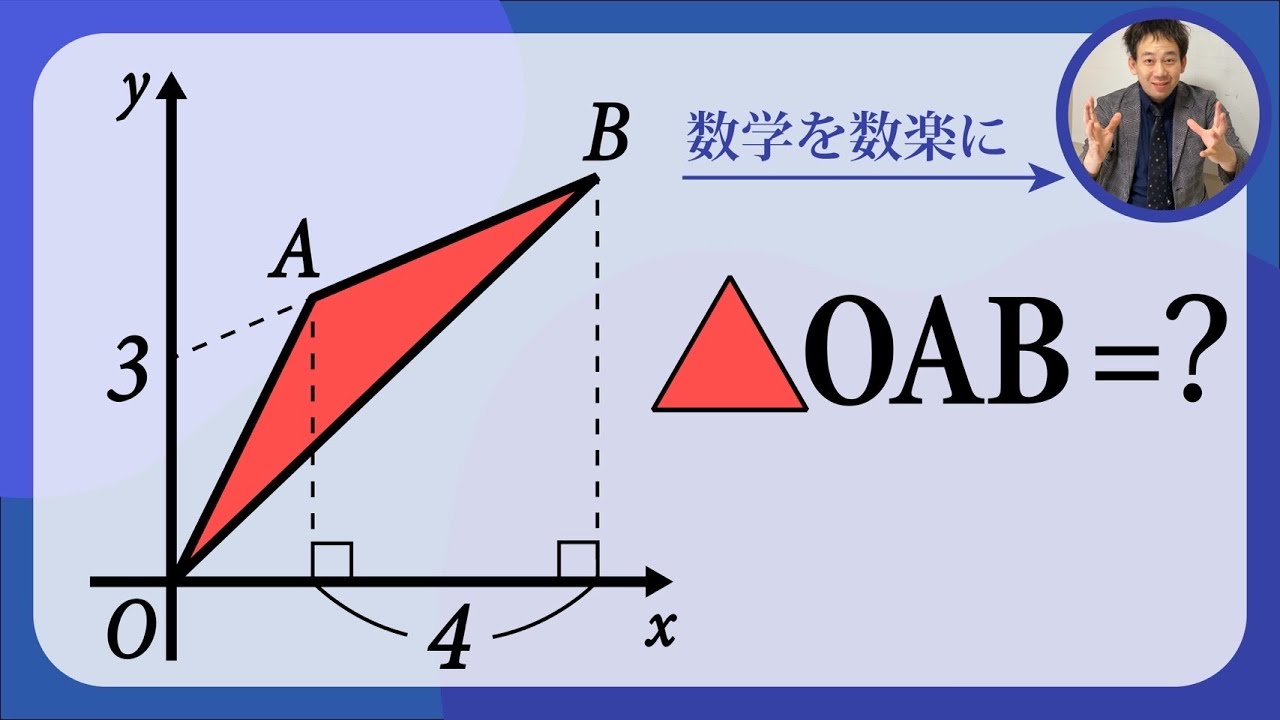
問題文全文(内容文):
$\overrightarrow{ OA }=\vec{ a },\overrightarrow{ OB }=\vec{ b }$のとき
$\overrightarrow{ OP }$を$\vec{ a },\vec{ b }$で表せ。
$\overrightarrow{ OA }=\vec{ a },\overrightarrow{ OB }=\vec{ b }$のとき
$\overrightarrow{ OP }$を$\vec{ a },\vec{ b }$で表せ。
単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
数学を数楽に
問題文全文(内容文):
$\overrightarrow{ OA }=\vec{ a },\overrightarrow{ OB }=\vec{ b }$のとき
$\overrightarrow{ OP }$を$\vec{ a },\vec{ b }$で表せ。
$\overrightarrow{ OA }=\vec{ a },\overrightarrow{ OB }=\vec{ b }$のとき
$\overrightarrow{ OP }$を$\vec{ a },\vec{ b }$で表せ。
投稿日:2019.12.29