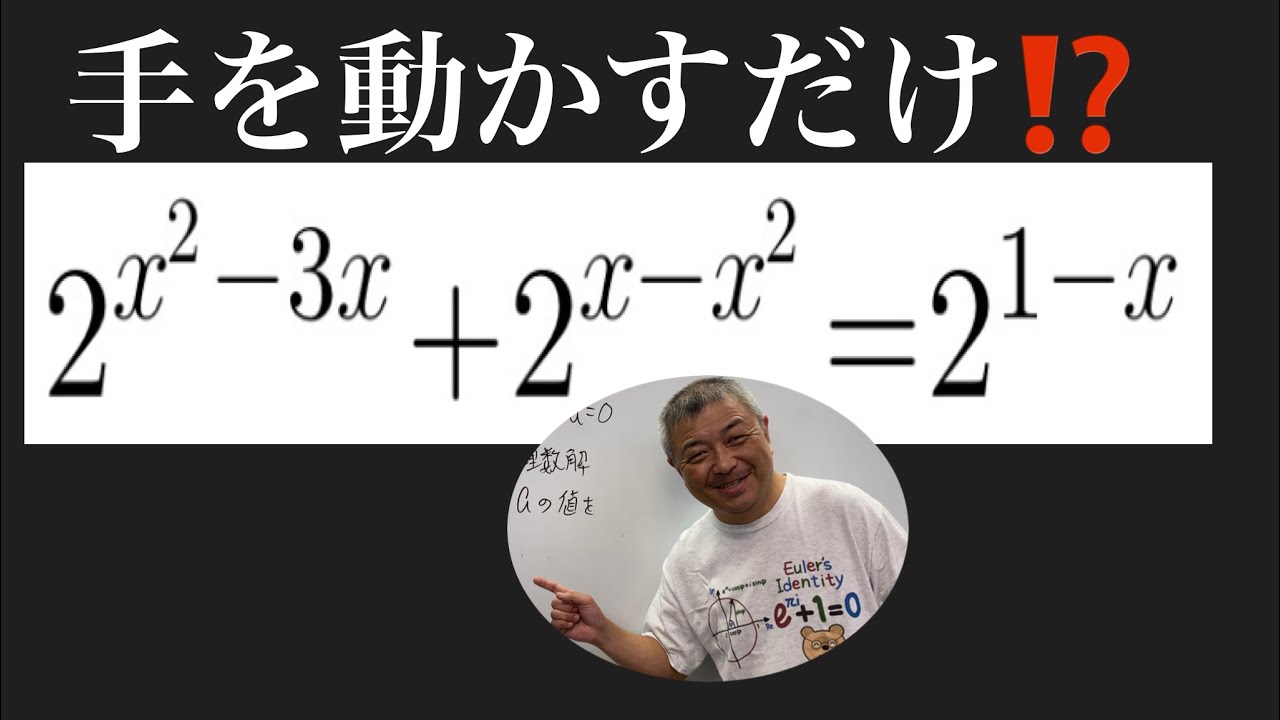問題文全文(内容文):
$ x^2-25x+143=0,(x-16)^2-\dfrac{1}{(x-16)^2}$
の値を求めよ.
$ x^2-25x+143=0,(x-16)^2-\dfrac{1}{(x-16)^2}$
の値を求めよ.
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^2-25x+143=0,(x-16)^2-\dfrac{1}{(x-16)^2}$
の値を求めよ.
$ x^2-25x+143=0,(x-16)^2-\dfrac{1}{(x-16)^2}$
の値を求めよ.
投稿日:2022.08.27