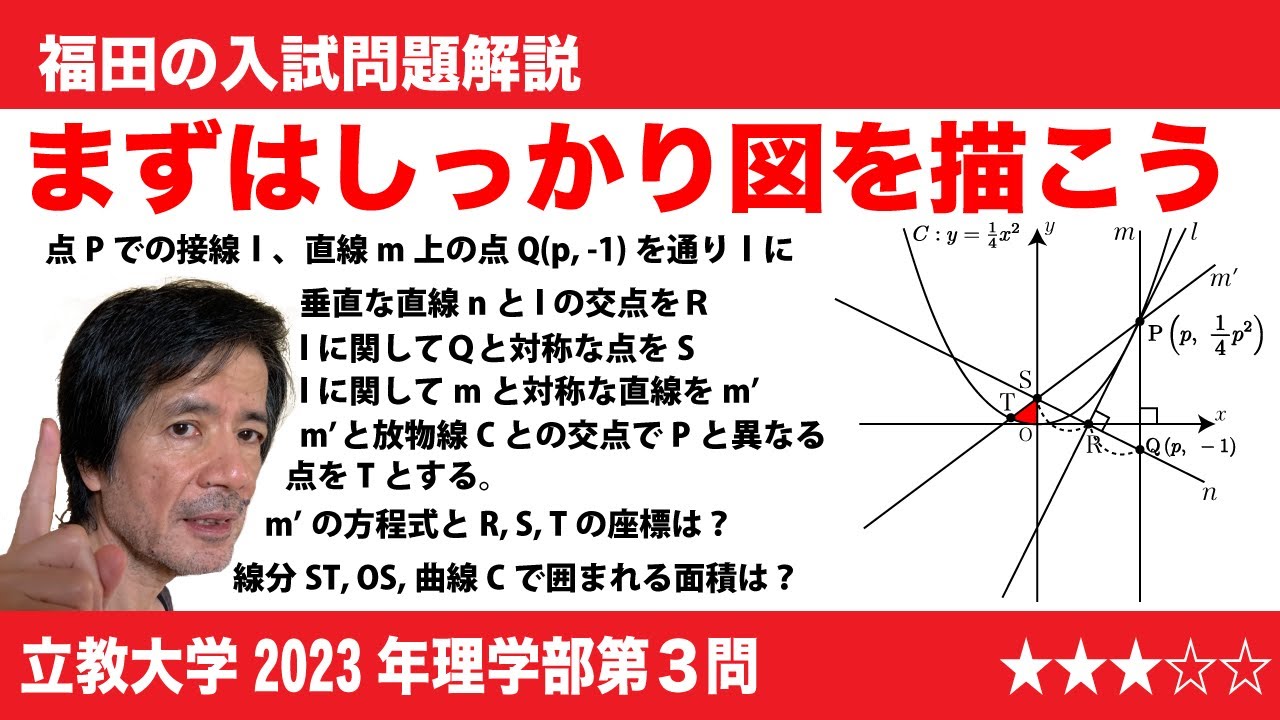
問題文全文(内容文):
${\Large\boxed{4}}$a
aを正の実数、bを1より大きい実数としたとき、放物線$y=-ax^2+b$が、
下図(※動画参照)のように原点を中心とした半径1の円$x^2+y^2=1$と2箇所で
接している。(すなわち共有点において共通の接線を持つ)
(1)一般に、$b=\frac{\boxed{\ \ アイ\ \ }a^2+\boxed{\ \ ウエ\ \ }a+\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }a+\boxed{\ \ ケコ\ \ }}$である。
(2)特に、$a=\frac{\sqrt2}{2}$とすると、放物線と円の接点は
$(±\frac{\sqrt{\boxed{\ \ サシ\ \ }}}{\boxed{\ \ スセ\ \ }},\ \frac{\sqrt{\boxed{\ \ ソタ\ \ }}}{\boxed{\ \ チツ\ \ }})$
であり、円と放物線に囲まれた上図の斜線部の面積は
$\frac{\boxed{\ \ テト\ \ }+\boxed{\ \ ナニ\ \ }\pi}{\boxed{\ \ ヌネ\ \ }}$となる。
2021慶應義塾大学総合政策学部過去問
${\Large\boxed{4}}$a
aを正の実数、bを1より大きい実数としたとき、放物線$y=-ax^2+b$が、
下図(※動画参照)のように原点を中心とした半径1の円$x^2+y^2=1$と2箇所で
接している。(すなわち共有点において共通の接線を持つ)
(1)一般に、$b=\frac{\boxed{\ \ アイ\ \ }a^2+\boxed{\ \ ウエ\ \ }a+\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }a+\boxed{\ \ ケコ\ \ }}$である。
(2)特に、$a=\frac{\sqrt2}{2}$とすると、放物線と円の接点は
$(±\frac{\sqrt{\boxed{\ \ サシ\ \ }}}{\boxed{\ \ スセ\ \ }},\ \frac{\sqrt{\boxed{\ \ ソタ\ \ }}}{\boxed{\ \ チツ\ \ }})$
であり、円と放物線に囲まれた上図の斜線部の面積は
$\frac{\boxed{\ \ テト\ \ }+\boxed{\ \ ナニ\ \ }\pi}{\boxed{\ \ ヌネ\ \ }}$となる。
2021慶應義塾大学総合政策学部過去問
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$a
aを正の実数、bを1より大きい実数としたとき、放物線$y=-ax^2+b$が、
下図(※動画参照)のように原点を中心とした半径1の円$x^2+y^2=1$と2箇所で
接している。(すなわち共有点において共通の接線を持つ)
(1)一般に、$b=\frac{\boxed{\ \ アイ\ \ }a^2+\boxed{\ \ ウエ\ \ }a+\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }a+\boxed{\ \ ケコ\ \ }}$である。
(2)特に、$a=\frac{\sqrt2}{2}$とすると、放物線と円の接点は
$(±\frac{\sqrt{\boxed{\ \ サシ\ \ }}}{\boxed{\ \ スセ\ \ }},\ \frac{\sqrt{\boxed{\ \ ソタ\ \ }}}{\boxed{\ \ チツ\ \ }})$
であり、円と放物線に囲まれた上図の斜線部の面積は
$\frac{\boxed{\ \ テト\ \ }+\boxed{\ \ ナニ\ \ }\pi}{\boxed{\ \ ヌネ\ \ }}$となる。
2021慶應義塾大学総合政策学部過去問
${\Large\boxed{4}}$a
aを正の実数、bを1より大きい実数としたとき、放物線$y=-ax^2+b$が、
下図(※動画参照)のように原点を中心とした半径1の円$x^2+y^2=1$と2箇所で
接している。(すなわち共有点において共通の接線を持つ)
(1)一般に、$b=\frac{\boxed{\ \ アイ\ \ }a^2+\boxed{\ \ ウエ\ \ }a+\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }a+\boxed{\ \ ケコ\ \ }}$である。
(2)特に、$a=\frac{\sqrt2}{2}$とすると、放物線と円の接点は
$(±\frac{\sqrt{\boxed{\ \ サシ\ \ }}}{\boxed{\ \ スセ\ \ }},\ \frac{\sqrt{\boxed{\ \ ソタ\ \ }}}{\boxed{\ \ チツ\ \ }})$
であり、円と放物線に囲まれた上図の斜線部の面積は
$\frac{\boxed{\ \ テト\ \ }+\boxed{\ \ ナニ\ \ }\pi}{\boxed{\ \ ヌネ\ \ }}$となる。
2021慶應義塾大学総合政策学部過去問
投稿日:2021.07.19