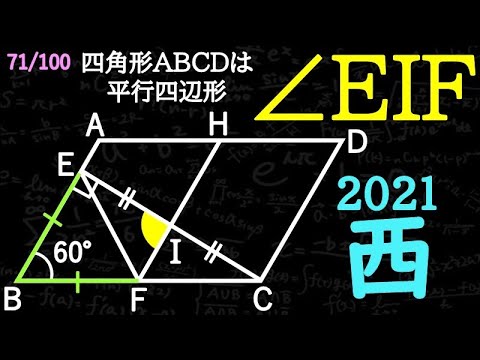
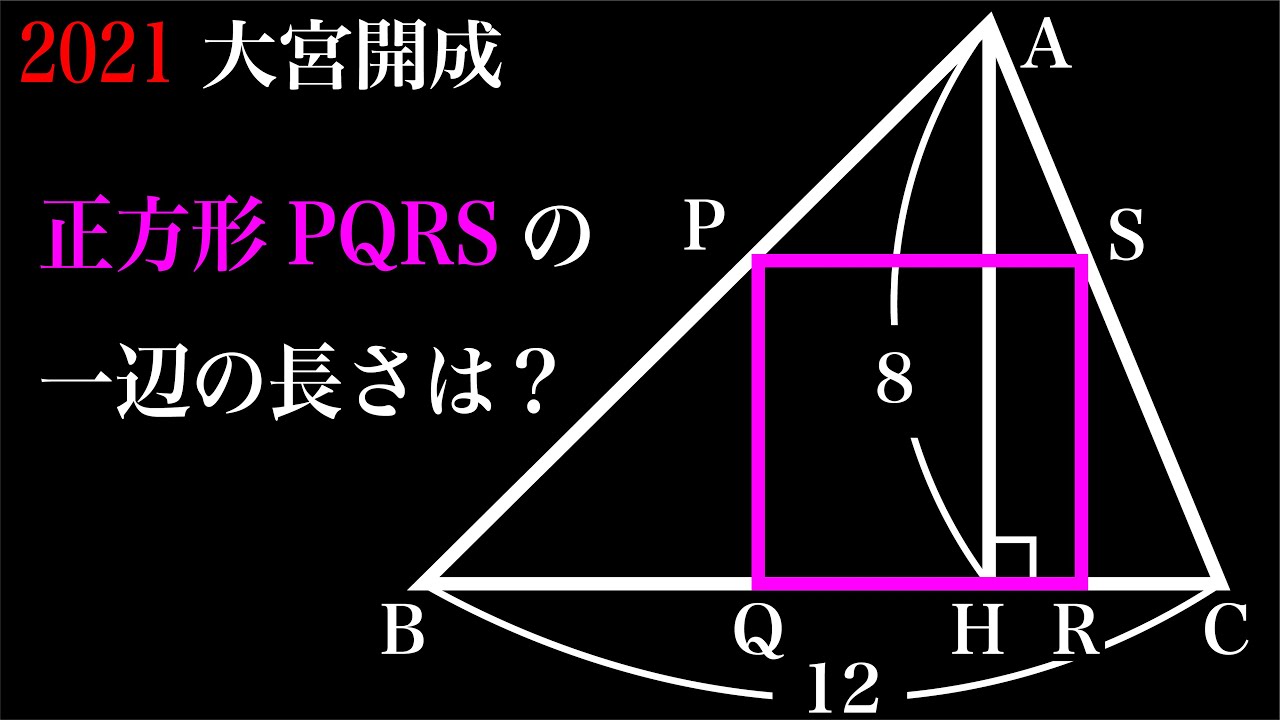
問題文全文(内容文):
校受験対策・確率7
Q
表に1と書かれたコインが1枚、2と書かれたコインが1枚、4と書かれたコインが1枚の合計3枚のコインがある。
いずれのコインも裏には何も書かれていない。
この3枚のコインを同時に投げるとき、①②の問いに答えなさい。
ただし、いずれのコインも表裏の出かたは同様に確からしいものとする。
①表裏の出かたは全部で何通りあるか、求めなさい。
②表が出たコインに書かれた数の和が、4以上になる確率を求めなさい。
Q
表に1と書かれたコインが1枚、2と書かれたコインが2枚、4と書かれたコインが1枚の合計4枚のコインが ある。
いずれのコインも裏には何も書かれていない。
この4枚のコインを同時に投げるとき、③、④の問いに答え なさい。
ただし、いずれのコインも表裏の出かたは同様に確からしいものとする。
③表が出たコインに書かれた数の和が、4になる確率を求めなさい。
④表が出たコインに書かれた数の和が、4以上になる確率を求めなさい。
校受験対策・確率7
Q
表に1と書かれたコインが1枚、2と書かれたコインが1枚、4と書かれたコインが1枚の合計3枚のコインがある。
いずれのコインも裏には何も書かれていない。
この3枚のコインを同時に投げるとき、①②の問いに答えなさい。
ただし、いずれのコインも表裏の出かたは同様に確からしいものとする。
①表裏の出かたは全部で何通りあるか、求めなさい。
②表が出たコインに書かれた数の和が、4以上になる確率を求めなさい。
Q
表に1と書かれたコインが1枚、2と書かれたコインが2枚、4と書かれたコインが1枚の合計4枚のコインが ある。
いずれのコインも裏には何も書かれていない。
この4枚のコインを同時に投げるとき、③、④の問いに答え なさい。
ただし、いずれのコインも表裏の出かたは同様に確からしいものとする。
③表が出たコインに書かれた数の和が、4になる確率を求めなさい。
④表が出たコインに書かれた数の和が、4以上になる確率を求めなさい。
単元:
#数学(中学生)#中2数学#確率
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
校受験対策・確率7
Q
表に1と書かれたコインが1枚、2と書かれたコインが1枚、4と書かれたコインが1枚の合計3枚のコインがある。
いずれのコインも裏には何も書かれていない。
この3枚のコインを同時に投げるとき、①②の問いに答えなさい。
ただし、いずれのコインも表裏の出かたは同様に確からしいものとする。
①表裏の出かたは全部で何通りあるか、求めなさい。
②表が出たコインに書かれた数の和が、4以上になる確率を求めなさい。
Q
表に1と書かれたコインが1枚、2と書かれたコインが2枚、4と書かれたコインが1枚の合計4枚のコインが ある。
いずれのコインも裏には何も書かれていない。
この4枚のコインを同時に投げるとき、③、④の問いに答え なさい。
ただし、いずれのコインも表裏の出かたは同様に確からしいものとする。
③表が出たコインに書かれた数の和が、4になる確率を求めなさい。
④表が出たコインに書かれた数の和が、4以上になる確率を求めなさい。
校受験対策・確率7
Q
表に1と書かれたコインが1枚、2と書かれたコインが1枚、4と書かれたコインが1枚の合計3枚のコインがある。
いずれのコインも裏には何も書かれていない。
この3枚のコインを同時に投げるとき、①②の問いに答えなさい。
ただし、いずれのコインも表裏の出かたは同様に確からしいものとする。
①表裏の出かたは全部で何通りあるか、求めなさい。
②表が出たコインに書かれた数の和が、4以上になる確率を求めなさい。
Q
表に1と書かれたコインが1枚、2と書かれたコインが2枚、4と書かれたコインが1枚の合計4枚のコインが ある。
いずれのコインも裏には何も書かれていない。
この4枚のコインを同時に投げるとき、③、④の問いに答え なさい。
ただし、いずれのコインも表裏の出かたは同様に確からしいものとする。
③表が出たコインに書かれた数の和が、4になる確率を求めなさい。
④表が出たコインに書かれた数の和が、4以上になる確率を求めなさい。
投稿日:2020.01.16