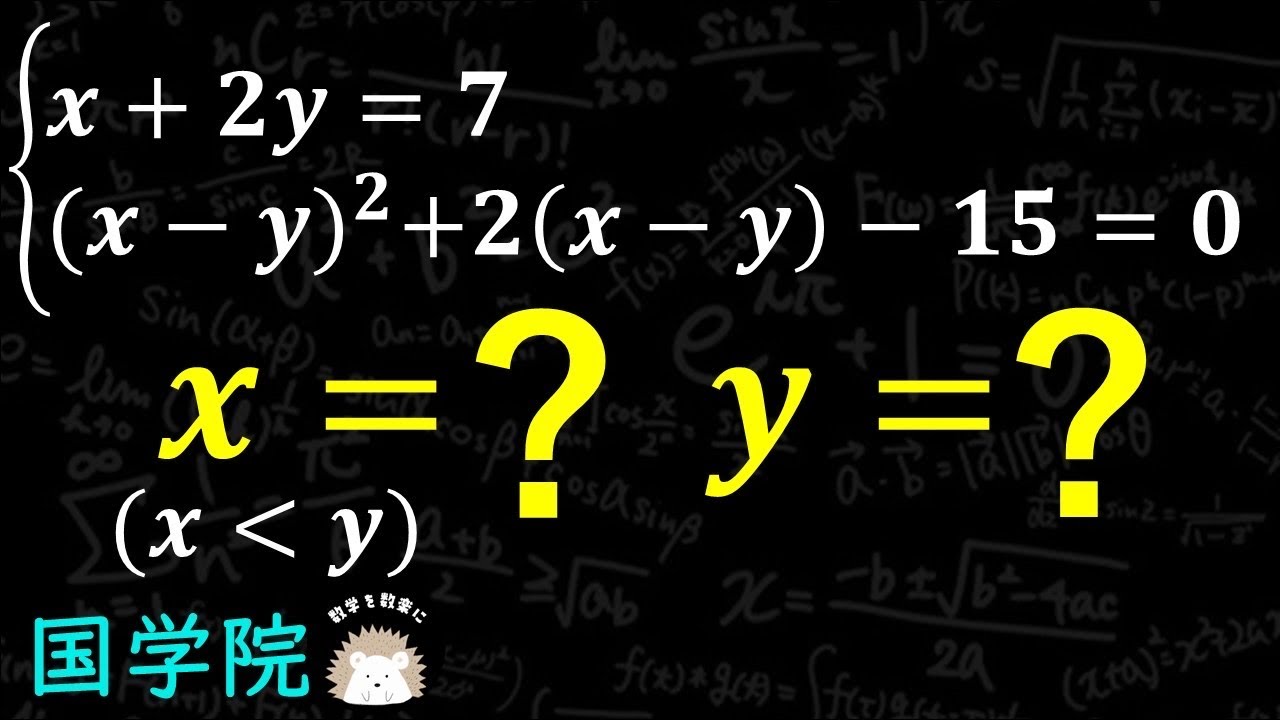サクッとスッキリ

問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
a+\dfrac{1}{c}=1 \\
b+\dfrac{1}{a}=1\\
c+\dfrac{1}{b}=5 \\
\end{array}
\right.
\end{eqnarray}$

$abc$はいくつか?

単元： #2次方程式と2次不等式

指導講師：鈴木貫太郎

問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
a+\dfrac{1}{c}=1 \\
b+\dfrac{1}{a}=1\\
c+\dfrac{1}{b}=5 \\
\end{array}
\right.
\end{eqnarray}$

$abc$はいくつか?

投稿日：2022.05.09

＜関連動画＞

産業医大　３次方程式と２次方程式の共通解

単元： #数Ⅰ#数Ⅱ#２次関数#複素数と方程式#2次方程式と2次不等式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$P$は素数であり,$q$は整数である.
$x^3-2x^2+x-p=0$,$x^2-x+q=0$が1つの共通解をもつ,$p,q$を求めよ.

1996産業医大過去問

この動画を見る　

福田の数学〜中央大学2021年経済学部第１問(1)〜2次方程式の解

単元： #数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#2次方程式と2次不等式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)

指導講師： JiroFukuda Math Channel

問題文全文(内容文)：
$\boxed{1}$(1)次の2次方程式において,1つの解が$x=\dfrac{3}{2}-i$であるとき,
実数$a,b$の値を求めよ.ただし,$i$は虚数単位とする.
$-x^2+ax+b=0$

2021中央大経済学部過去問

この動画を見る　

【数Ⅰ】2次方程式の解の配置問題【問題文を図にしよう】

単元： #数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)

指導講師：めいちゃんねる

問題文全文(内容文)：
$ 2次方程式x^2-2ax+a+2=0の異なる2つの実数解が以下の条件を満たすとき定数aの値の範囲を求めよ.
(1)ともに1より大きい.
(2)一方が1より小さく,他方が1より大きい.$

この動画を見る　

一文字削除からの判別式【2014年早稲田大学】

単元： #数Ⅰ#大学入試過去問(数学)#数と式#２次関数#式の計算（整式・展開・因数分解）#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)

指導講師：数学・算数の楽しさを思い出した / Ken

問題文全文(内容文)：
実数$a,b,c$が
$a+b+c=8,a^2+b^2+c^2=32$
を満たす時、実数$c$の最大値を求めよ。

2014早稲田大過去問

この動画を見る　

【数Ⅰ】高2生必見!!2020年度第2回 K塾高2模試大問2-1_2次関数

単元： #数Ⅰ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#全統模試(河合塾)#数学(高校生)

指導講師：理数個別チャンネル

問題文全文(内容文)：
実数xについての2つの不等式$ ax^2+2ax-2a+1\leqq 0$・・・①
$\vert x-2\vert \leqq 1$・・・② がある。
ただし、aは0でない実数の定数とする。
(1)$a=-1$のとき、①を解け。
(2)②を解け。
(3)②を満たすすべてのxが①を満たすようなaの値の範囲を求めよ。

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> サクッとスッキリ

＜関連動画＞

産業医大 ３次方程式と２次方程式の共通解

福田の数学〜中央大学2021年経済学部第１問(1)〜2次方程式の解

【数Ⅰ】2次方程式の解の配置問題【問題文を図にしよう】

一文字削除からの判別式【2014年早稲田大学】

【数Ⅰ】高2生必見!!2020年度 第2回 K塾高2模試 大問2-1_2次関数