2次方程式と2次不等式
2次方程式と2次不等式
2次方程式x²+2mx+2m+3=0が次のような実数解をもつように、定数mの値の範囲を定めよ。 (1)異なる2つの負の解 (2)-4より大きい異なる2つの解【数Ⅰ】【2次関数｜2次不等式応用】
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2次方程式 $x^{2}+2mx+2m+3=0$ が次のような実数解をもつように、定数 $m$ の値の範囲を定めよ。
(1) 異なる2つの負の解
(2) $-4$ より大きい異なる2つの解
この動画を見る
2次方程式 $x^{2}+2mx+2m+3=0$ が次のような実数解をもつように、定数 $m$ の値の範囲を定めよ。
(1) 異なる2つの負の解
(2) $-4$ より大きい異なる2つの解
不等式x²-(a+1)x+a＜0を満たす整数xがちょうど2個だけ存在するように、定数aの値の範囲を定めよ。【数Ⅰ】【2次関数｜2次不等式応用】
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
不等式 $x^{2}-(a+1)x+a<0$ を満たす整数 $x$ がちょうど2個だけ存在するように、定数 $a$ の値の範囲を定めよ。
この動画を見る
不等式 $x^{2}-(a+1)x+a<0$ を満たす整数 $x$ がちょうど2個だけ存在するように、定数 $a$ の値の範囲を定めよ。
次のxについての不等式を解け。(1)x²-(a+2)x+2a＜0 (2)x²-(a-1)x-a＞0 (3)x²-ax-2a²≦0【数Ⅰ】【2次関数｜2次不等式応用】
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の $x$ についての不等式を解け。
(1) $x^{2}-(a+2)x+2a<0$
(2) $x^{2}-(a-1)x-a>0$
(3) $x^{2}-ax-2a^{2}\leqq0$
この動画を見る
次の $x$ についての不等式を解け。
(1) $x^{2}-(a+2)x+2a<0$
(2) $x^{2}-(a-1)x-a>0$
(3) $x^{2}-ax-2a^{2}\leqq0$
2つの2次方程式x²+mx+m=0…①、x²-2mx+m+6=0…②がある。次の条件を満たすように、定数mの値の範囲を定めよ。（以下略）【数Ⅰ】【2次関数｜2次不等式応用】
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2つの2次方程式 $x^{2}+mx+m=0\cdots\cdots①$、$x^{2}-2mx+m+6=0\cdots\cdots②$ がる。次の条件を満たすように、定数 $m$ の値の範囲を定めよ。
(1) ①、②がともに異なる2つの実数解をもつ。
(2) ①、②がともに実数解をもたない。
(3) ①、②の少なくとも一方が実数解をもつ。
(4) ①、②のうち一方だけが、異なる2つの実数解をもつ。
この動画を見る
2つの2次方程式 $x^{2}+mx+m=0\cdots\cdots①$、$x^{2}-2mx+m+6=0\cdots\cdots②$ がる。次の条件を満たすように、定数 $m$ の値の範囲を定めよ。
(1) ①、②がともに異なる2つの実数解をもつ。
(2) ①、②がともに実数解をもたない。
(3) ①、②の少なくとも一方が実数解をもつ。
(4) ①、②のうち一方だけが、異なる2つの実数解をもつ。
a,bは定数とする。2次不等式4x²+ax+b＜0の解が1＜x＜5/4であるとき、2次不等式bx²+ax+4≧0の解を求めよ。【数Ⅰ】【2次関数｜2次不等式応用】
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
2次不等式ax²+x+b＞0の解がx＜-3,2＜xであるとき、定数a,bの値を求めよ。【数Ⅰ】【2次関数｜2次不等式応用】
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
和が20である2つの整数の積が96以上になるとき、この2つの整数の組をすべて求めよ。【数Ⅰ】【2次関数｜2次不等式文章問題】
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
和が20である2つの整数の積が96以上になるとき、この2つの整数の組をすべて求めよ。
この動画を見る
和が20である2つの整数の積が96以上になるとき、この2つの整数の組をすべて求めよ。
立方体の縦を1cm短くし、横はそのまま、高さは2cm長くして直方体を作る。このとき、直方体の体積がもとの立方体の体積より大きくならないのは、（以下略）【数Ⅰ】【2次関数｜2次不等式文章問題】
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
立方体の縦を $1\text{cm}$ 短くし、横はそのまま、高さは $2\text{cm}$ 長くして直方体を作る。このとき、直方体の体積がもとの立方体の体積より大きくならないのは、もとの立方体の1辺の長さがどのような範囲にあるときか。
この動画を見る
立方体の縦を $1\text{cm}$ 短くし、横はそのまま、高さは $2\text{cm}$ 長くして直方体を作る。このとき、直方体の体積がもとの立方体の体積より大きくならないのは、もとの立方体の1辺の長さがどのような範囲にあるときか。
次の連立不等式を満たす整数xの値を全て求めよ。(1) 2x²-x-3＜0, 3x²-10x+3＜0 (2) x²+2x＞1, x²-x≦6【数Ⅰ】【2次関数｜解の個数、連立】
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の連立不等式を満たす整数 $x$ の値をすべて求めよ。
(1) $2x^{2}-x-3<0$、$3x^{2}-10x+3<0$
(2) $x^{2}+2x>1$、$x^{2}-x\leqq6$
この動画を見る
次の連立不等式を満たす整数 $x$ の値をすべて求めよ。
(1) $2x^{2}-x-3<0$、$3x^{2}-10x+3<0$
(2) $x^{2}+2x>1$、$x^{2}-x\leqq6$
x² + (m + 3)x + 8 = 0, x² + 5x + 4m = 0 が共通な実数解をもつように定数ｍの値を定め, その共通な解を求めよ。【数Ⅰ】【2次関数｜文字を含む2次方程式 】
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2つの2次方程式 $x^{2}+(m+3)x+8=0$、$x^{2}+5x+4m=0$ が共通な実数解をもつように定数 $m$ の値を定め、その共通な解を求めよ。
この動画を見る
2つの2次方程式 $x^{2}+(m+3)x+8=0$、$x^{2}+5x+4m=0$ が共通な実数解をもつように定数 $m$ の値を定め、その共通な解を求めよ。
aを定数とするとき，次の方程式を解け。(1) a²x + 1 = a(x + 1) (2) ax² + (a² - 1)x - a = 0 【数Ⅰ】【2次関数｜文字を含む2次方程式】
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$aを定数とするとき,\ 次の方程式を解け。\\$
$(1)\ a^{2}x+1=a(x+1)\\$
$(2)\ ax^{2}+(a^{2}-1)x-a=0$
この動画を見る
$aを定数とするとき,\ 次の方程式を解け。\\$
$(1)\ a^{2}x+1=a(x+1)\\$
$(2)\ ax^{2}+(a^{2}-1)x-a=0$
x≧0, y≧0, x+y=4のとき，xのとりうる値の範囲を求めよ。また、x²+2y²の最大値と最小値を求めよ。【数Ⅰ】【2次関数｜2次関数の最大と最小条件式付き】
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$x\geqq0$、$y\geqq0$、$x+y=4$ のとき、$x$ のとりうる値の範囲を求めよ。また、$x^{2}+2y^{2}$ の最大値と最小値を求めよ。
この動画を見る
$x\geqq0$、$y\geqq0$、$x+y=4$ のとき、$x$ のとりうる値の範囲を求めよ。また、$x^{2}+2y^{2}$ の最大値と最小値を求めよ。
(1) 2x+y=1のとき，x²＋y²の最小値を求めよ。(2) x+2y+3=0のとき，xyの最大値を求めよ。【数Ⅰ】【2次関数｜2次関数の最大と最小条件式付き】
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
(1) $2x+y=1$ のとき、$x^{2}+y^{2}$ の最小値を求めよ。
(2) $x+2y+3=0$ のとき、$xy$ の最大値を求めよ。
この動画を見る
(1) $2x+y=1$ のとき、$x^{2}+y^{2}$ の最小値を求めよ。
(2) $x+2y+3=0$ のとき、$xy$ の最大値を求めよ。
このタイプの2次方程式の解き方は？
これの何が間違い？
福田のおもしろ数学516〜2次方程式が自然数解を持つ条件
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x^2-2ax+b=0$
$x^2-2bx+c=0$
$x^2-2cx+a=0$
がすべて自然数解をもつ。
このような自然数の組$(a,b,c)$を
すべて求めて下さい。
この動画を見る
$x^2-2ax+b=0$
$x^2-2bx+c=0$
$x^2-2cx+a=0$
がすべて自然数解をもつ。
このような自然数の組$(a,b,c)$を
すべて求めて下さい。
福田の数学〜慶應義塾大学薬学部2025第1問(1)〜絶対不等式と2次関数の最大最小
単元：
#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(1)$a$を実数とする。
$x$の$2$次関数$f(x)＝x^2-ax+a+2$は、
すべての実数$x$に対して$f(x)\geqq 0$を満たす。
(i)$a$の値の範囲は$\boxed{ア}$である。
(ii)$-2\leqq x\leqq 3$において、$f(x)$の最大値を$m$,
最大値を$M$とおく。
$m$が最大となるのは$a=\boxed{イ}$のときであり、
このとき$m=\boxed{ウ},M=\boxed{エ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{1}$
(1)$a$を実数とする。
$x$の$2$次関数$f(x)＝x^2-ax+a+2$は、
すべての実数$x$に対して$f(x)\geqq 0$を満たす。
(i)$a$の値の範囲は$\boxed{ア}$である。
(ii)$-2\leqq x\leqq 3$において、$f(x)$の最大値を$m$,
最大値を$M$とおく。
$m$が最大となるのは$a=\boxed{イ}$のときであり、
このとき$m=\boxed{ウ},M=\boxed{エ}$である。
$2025$年慶應義塾大学薬学部過去問題
【数Ⅰ】【2次関数】2次関数 条件付きの解 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の条件を満たすように、定数mの値の範囲を定めよ。
(1) ２次関数 y=x²+mx+1において、yの値が常に正である。
(2) 放物線 y=x²-2mx+3m-2がy＜0の部分を通らない。
(3) 関数 y=mx²+4x+m-3において、yの値が常に負である。
２次関数 y=x²-mx+m+3のグラフの頂点が第１象限にあるとき、定数mの値の範囲を求めよ。
この動画を見る
次の条件を満たすように、定数mの値の範囲を定めよ。
(1) ２次関数 y=x²+mx+1において、yの値が常に正である。
(2) 放物線 y=x²-2mx+3m-2がy＜0の部分を通らない。
(3) 関数 y=mx²+4x+m-3において、yの値が常に負である。
２次関数 y=x²-mx+m+3のグラフの頂点が第１象限にあるとき、定数mの値の範囲を求めよ。
【数Ⅰ】【2次関数】2次関数 解の個数、連立 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
mは定数とする。放物線 y=x²+(m+3)x+3m+4とx軸の共有点の個数を調べよ。
次の2次不等式の解がすべての実数であるとき、定数mの値の範囲を求めよ。
(1) x²-mx+1＞0 (2) -x²+mx+2m≦0
次の連立不等式を満たす整数xの値を全て求めよ。
(1) 2x²-x-3＜0 (2) x²+2x＞1
3x²-10x+3＜0 x²-x≦6
この動画を見る
mは定数とする。放物線 y=x²+(m+3)x+3m+4とx軸の共有点の個数を調べよ。
次の2次不等式の解がすべての実数であるとき、定数mの値の範囲を求めよ。
(1) x²-mx+1＞0 (2) -x²+mx+2m≦0
次の連立不等式を満たす整数xの値を全て求めよ。
(1) 2x²-x-3＜0 (2) x²+2x＞1
3x²-10x+3＜0 x²-x≦6
【数Ⅰ】【2次関数】2次関数の解の範囲 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の2次方程式が実数解をもつように、実数ｍの値の範囲を定めよ。
(1) x²+2mx+3=0 (2) x²+mx+m=0
２次方程式 x²-2mx-4m=0 が次の条件を満たすように、定数mの値の範囲を定めよ。
(1) 異なる２つの実数解をもつ (2) 実数解をもたない
次の条件を満たすように、実数mの値の範囲を定めよ。
(1) ２次関数 y=x²-2mx+2m+3 のグラフがｘ軸と共有点をもつ。
(2) ２次関数 y=x²+2mx-m+2 のグラフがｘ軸と共有点をもたない。
この動画を見る
次の2次方程式が実数解をもつように、実数ｍの値の範囲を定めよ。
(1) x²+2mx+3=0 (2) x²+mx+m=0
２次方程式 x²-2mx-4m=0 が次の条件を満たすように、定数mの値の範囲を定めよ。
(1) 異なる２つの実数解をもつ (2) 実数解をもたない
次の条件を満たすように、実数mの値の範囲を定めよ。
(1) ２次関数 y=x²-2mx+2m+3 のグラフがｘ軸と共有点をもつ。
(2) ２次関数 y=x²+2mx-m+2 のグラフがｘ軸と共有点をもたない。
【数Ⅰ】【2次関数】2次関数の点の通過 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の条件を満たす放物線の方程式を求めよ。
(1) ３点(-4,0),(-2,0),(0,-4)を通る。
(2) 点(2,0)でｘ軸に接し、点(-2,12)を通る。
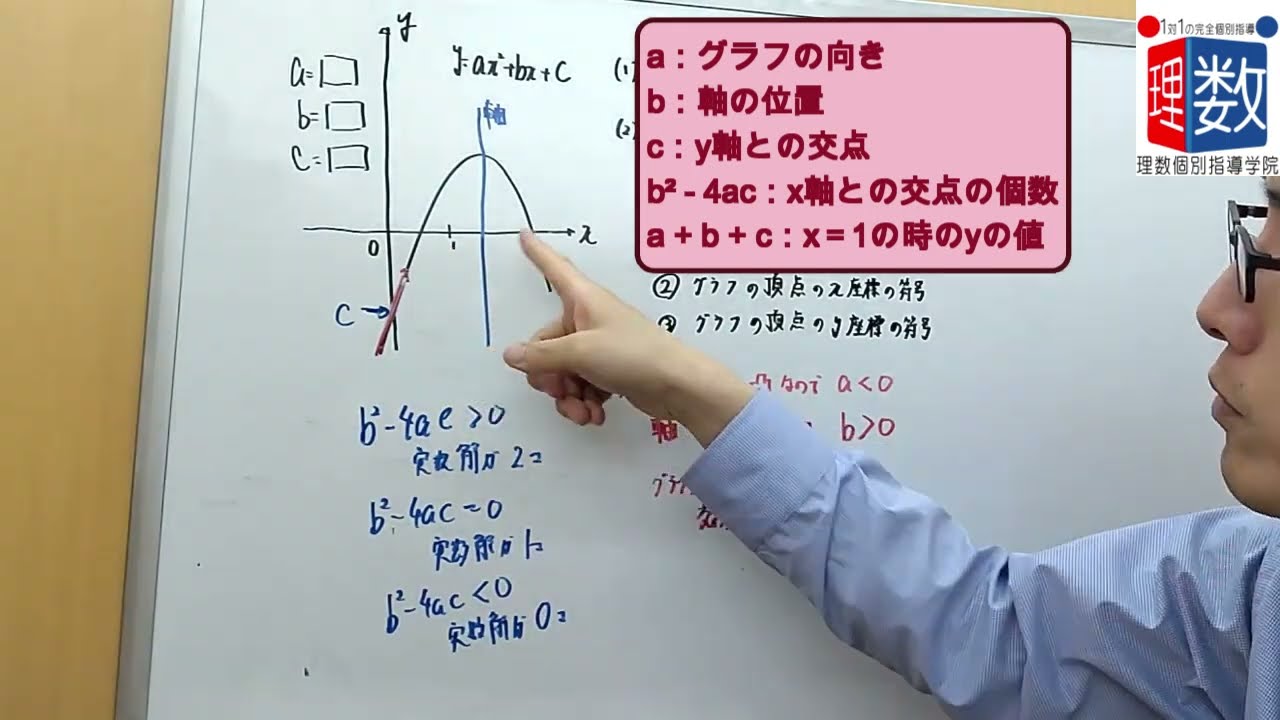
a,b,cの値を入力すると、関数 y=ax²+bx+c のグラフが表示されるコンピュータソフトがある。
あるa,b,cの値を入力すると、グラフは図のように表示された。
(1) a, b, c, b²-4ac, a+b+c の符号をいえ。
(2) このa,bの値を変えずに、cの値だけを変化させたとき、変わらないものを次の中からすべて選べ。
また、変わらない理由を説明せよ。
① グラフとｘ軸の共有点の個数
② グラフの頂点のｘ座標の符号
③ グラフの頂点のｙ座標の符号
この動画を見る
次の条件を満たす放物線の方程式を求めよ。
(1) ３点(-4,0),(-2,0),(0,-4)を通る。
(2) 点(2,0)でｘ軸に接し、点(-2,12)を通る。
a,b,cの値を入力すると、関数 y=ax²+bx+c のグラフが表示されるコンピュータソフトがある。
あるa,b,cの値を入力すると、グラフは図のように表示された。
(1) a, b, c, b²-4ac, a+b+c の符号をいえ。
(2) このa,bの値を変えずに、cの値だけを変化させたとき、変わらないものを次の中からすべて選べ。
また、変わらない理由を説明せよ。
① グラフとｘ軸の共有点の個数
② グラフの頂点のｘ座標の符号
③ グラフの頂点のｙ座標の符号
【数Ⅰ】【2次関数】2次関数のグラフ応用 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の2次関数のグラフがｘ軸から切り取る線分の長さを求めよ。
(1) y=x²-2x-8 (2) y=x²+6x+7
2次関数 y=x²-4x+2m のグラフとｘ軸の共有点の個数は，定数 m の値によってどのように変わるか。
この動画を見る
次の2次関数のグラフがｘ軸から切り取る線分の長さを求めよ。
(1) y=x²-2x-8 (2) y=x²+6x+7
2次関数 y=x²-4x+2m のグラフとｘ軸の共有点の個数は，定数 m の値によってどのように変わるか。
【数Ⅰ】【2次関数】文字を含む2次方程式 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
aを定数とするとき，次の方程式を解け。
(1) a²x + 1 = a(x + 1)
(2) ax² + (a² - 1)x - a = 0
２つの２次方程式 x² + (m + 3)x + 8 = 0, x² + 5x + 4m = 0 が共通な実数解をもつように
定数ｍの値を定め, その共通な解を求めよ。
この動画を見る
aを定数とするとき，次の方程式を解け。
(1) a²x + 1 = a(x + 1)
(2) ax² + (a² - 1)x - a = 0
２つの２次方程式 x² + (m + 3)x + 8 = 0, x² + 5x + 4m = 0 が共通な実数解をもつように
定数ｍの値を定め, その共通な解を求めよ。
【数Ⅰ】【2次関数】2次関数の決定 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の条件を満たすような放物線の方程式を求めよ。
(1) 放物線 y=-3x²+x-1を平行移動した曲線で，頂点が点(-2,3)である。
(2) 放物線 y=x²-3xを平行移動した曲線で，2点 (2,1),(4,5)を通る。
2つの放物線y=x²-3x, y=1/2x²+ax+bの頂点が一致するように,定数a,bの値を定めよ。
(1) 放物線y=x²-3x十4を平行移動した曲線で，点(2, 4)を通り，頂点が直線y=2x+1上にある放物線の方程式を求めよ。
(2) 放物線y=-2x²＋5xを平行移動した曲線で，点(1, -3)を通り，頂点が放物線y＝x²十4上にある放物線の方程式を求めよ。
この動画を見る
次の条件を満たすような放物線の方程式を求めよ。
(1) 放物線 y=-3x²+x-1を平行移動した曲線で，頂点が点(-2,3)である。
(2) 放物線 y=x²-3xを平行移動した曲線で，2点 (2,1),(4,5)を通る。
2つの放物線y=x²-3x, y=1/2x²+ax+bの頂点が一致するように,定数a,bの値を定めよ。
(1) 放物線y=x²-3x十4を平行移動した曲線で，点(2, 4)を通り，頂点が直線y=2x+1上にある放物線の方程式を求めよ。
(2) 放物線y=-2x²＋5xを平行移動した曲線で，点(1, -3)を通り，頂点が放物線y＝x²十4上にある放物線の方程式を求めよ。
【数Ⅰ】【2次関数】2次関数の最大と最小条件式付き ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
(1) 2x+y=1のとき，x²＋y²の最小値を求めよ。
(2) x+2y+3=0のとき，xyの最大値を求めよ。
x≧0, y≧0, x+y=4のとき，xのとりうる値の範囲を求めよ。また、x²+2y²の最大値と最小値を求めよ。
この動画を見る
(1) 2x+y=1のとき，x²＋y²の最小値を求めよ。
(2) x+2y+3=0のとき，xyの最大値を求めよ。
x≧0, y≧0, x+y=4のとき，xのとりうる値の範囲を求めよ。また、x²+2y²の最大値と最小値を求めよ。
2次方程式のこれ解ける？
単元：
#数学(中学生)#中３数学#２次方程式#数Ⅰ#２次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
aを定数とする。xの2次方程式
$3(x+a)^2 = (2a^2+1)(x+a)+x^2-2ax-3a^2$
が解を1つしかもたないようなaの値を全て求めよ。（灘高校 2024）
この動画を見る
aを定数とする。xの2次方程式
$3(x+a)^2 = (2a^2+1)(x+a)+x^2-2ax-3a^2$
が解を1つしかもたないようなaの値を全て求めよ。（灘高校 2024）
高２から東大に挑戦！二次方程式と対数の融合問題！基本がぎゅっと詰まってます【東京大学】【数学 入試問題】
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
2次方程式 x^2-2xloga_b+logb_a=0 が異なる実数解α,βをもち、0<α<1<β となるものとする。このときa,b,1の大きさの順序はどのようなものになるか？
この動画を見る
2次方程式 x^2-2xloga_b+logb_a=0 が異なる実数解α,βをもち、0<α<1<β となるものとする。このときa,b,1の大きさの順序はどのようなものになるか？
2次方程式の解を四捨五入！？あまり見かけない問題。解ける？ #Shorts #ずんだもん #勉強 #数学
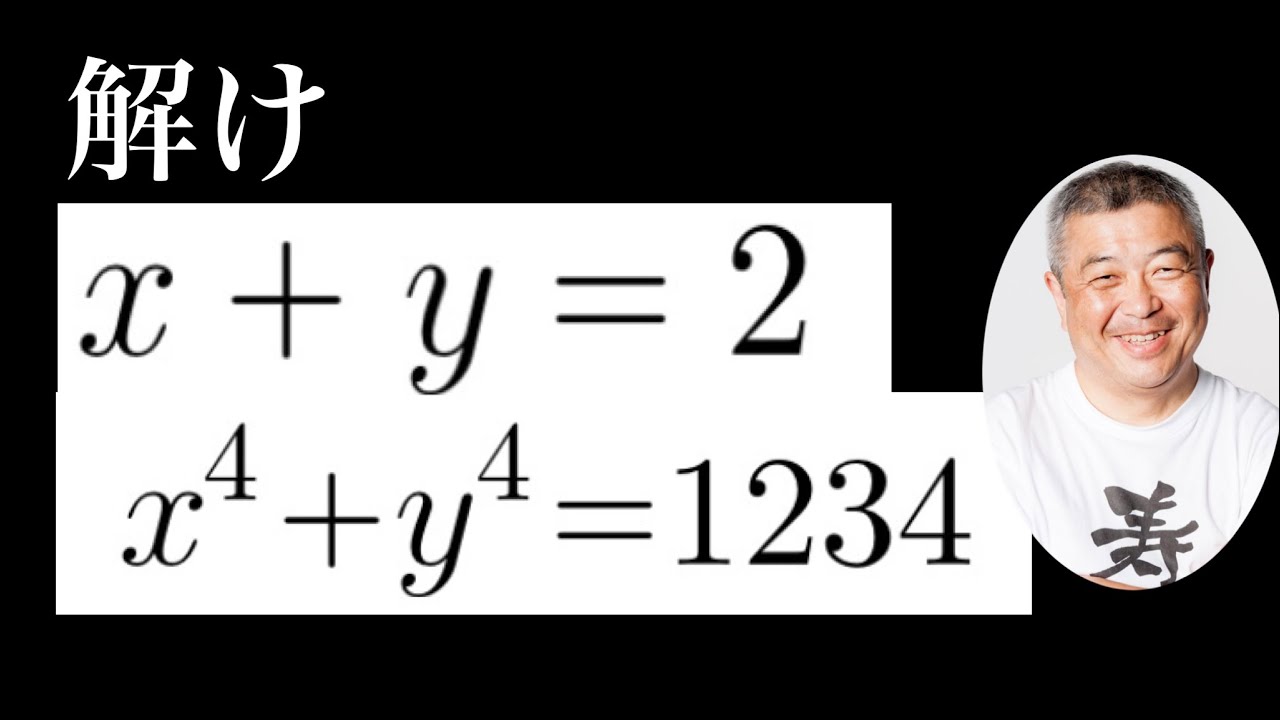
単元：
#数Ⅰ#数A#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
m,nを正の整数とする。xについての2次方程式 12x^2-mx+n=0 の2つの実数解を小数第2位で四捨五入して0.3および0.7を得た。m,nを求めよ。
この動画を見る
m,nを正の整数とする。xについての2次方程式 12x^2-mx+n=0 の2つの実数解を小数第2位で四捨五入して0.3および0.7を得た。m,nを求めよ。
【数Ⅰ】【2次関数】絶対値を含む関数のグラフ ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の関数のグラフをかけ。
(1)y=|2x+1|
(2)y=|x²+x|
(3)y=|x²-3x-4|
次の関数のグラフをかけ。
(1)y=x²-4|x|
(2)y=|x+1|(x-3)
次の関数のグラフをかけ。
(1)y=|x|+|x-1|
(2)y=|x+1|-|x-2|
この動画を見る
次の関数のグラフをかけ。
(1)y=|2x+1|
(2)y=|x²+x|
(3)y=|x²-3x-4|
次の関数のグラフをかけ。
(1)y=x²-4|x|
(2)y=|x+1|(x-3)
次の関数のグラフをかけ。
(1)y=|x|+|x-1|
(2)y=|x+1|-|x-2|
【数Ⅰ】【2次関数】2次不等式応用4 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2次関数y=x²+mx+2が次の条件を満たすように、定数mの値の範囲を定めよ。
(1)この2次関数のグラフとx軸の正の部分が異なる2点で交わる。
(2)この2次関数のグラフとx軸のx＜-1の部分が異なる2点で交わる。
放物線y=x²+2(m-1)x+5-m²がx軸の正の部分と負の部分のそれぞれと交わるように、定数mの値の範囲を定めよ。
2次方程式x²+2mx+2m+3=0が次のような実数解をもつように、定数mの値の範囲を定めよ。
(1)異なる2つの負の解
(2)-4より大きい異なる2つの解
この動画を見る
2次関数y=x²+mx+2が次の条件を満たすように、定数mの値の範囲を定めよ。
(1)この2次関数のグラフとx軸の正の部分が異なる2点で交わる。
(2)この2次関数のグラフとx軸のx＜-1の部分が異なる2点で交わる。
放物線y=x²+2(m-1)x+5-m²がx軸の正の部分と負の部分のそれぞれと交わるように、定数mの値の範囲を定めよ。
2次方程式x²+2mx+2m+3=0が次のような実数解をもつように、定数mの値の範囲を定めよ。
(1)異なる2つの負の解
(2)-4より大きい異なる2つの解