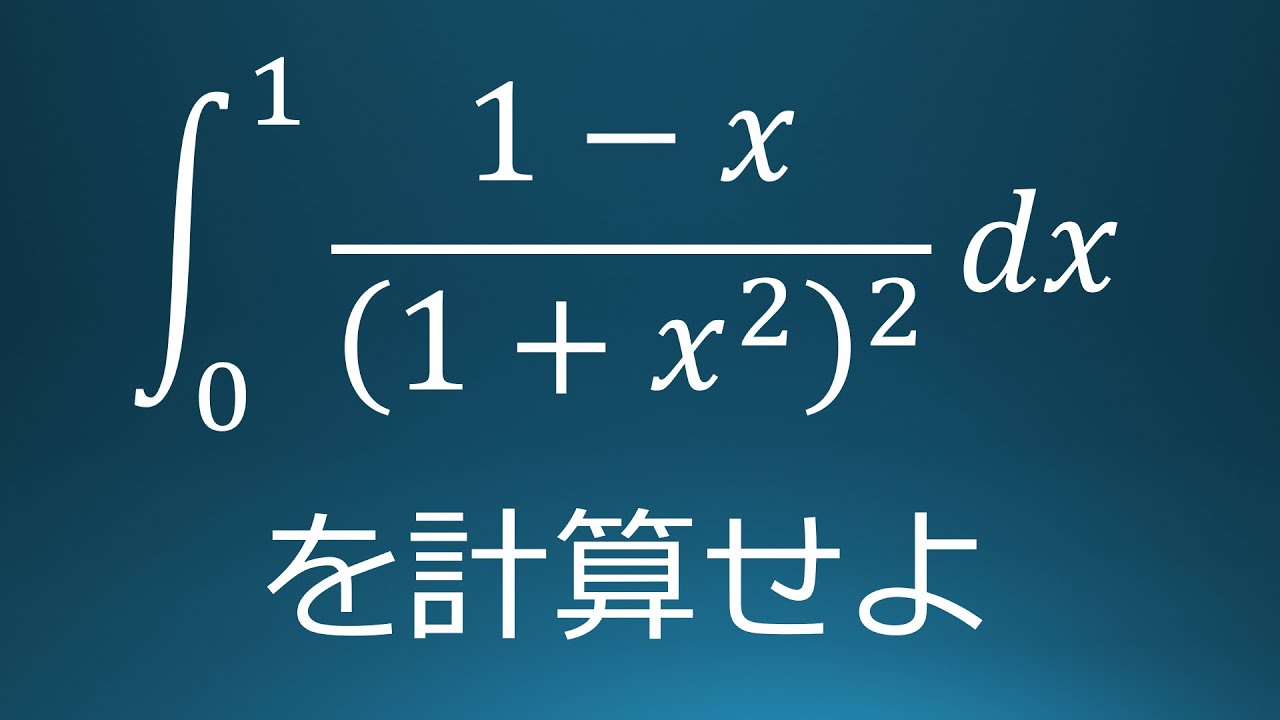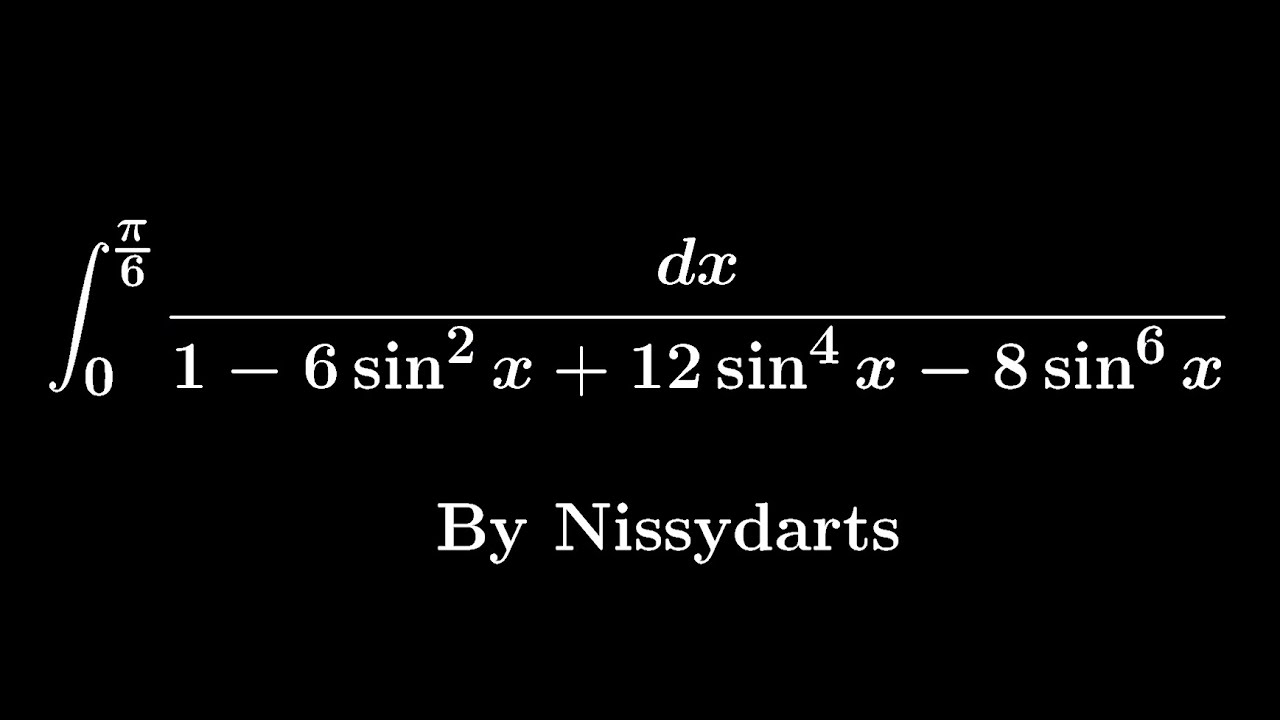問題文全文(内容文):
半径1の円を底面とする高さが$\sqrt3$の直円柱と、半径がrの球を考える。
直円柱の底面の中心と球の中心が一致するとき、直円柱の内部と球の内部の
共通部分の体積V(r)を求めよ。
2022東北大学理系過去問
半径1の円を底面とする高さが$\sqrt3$の直円柱と、半径がrの球を考える。
直円柱の底面の中心と球の中心が一致するとき、直円柱の内部と球の内部の
共通部分の体積V(r)を求めよ。
2022東北大学理系過去問
単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
半径1の円を底面とする高さが$\sqrt3$の直円柱と、半径がrの球を考える。
直円柱の底面の中心と球の中心が一致するとき、直円柱の内部と球の内部の
共通部分の体積V(r)を求めよ。
2022東北大学理系過去問
半径1の円を底面とする高さが$\sqrt3$の直円柱と、半径がrの球を考える。
直円柱の底面の中心と球の中心が一致するとき、直円柱の内部と球の内部の
共通部分の体積V(r)を求めよ。
2022東北大学理系過去問
投稿日:2022.03.25