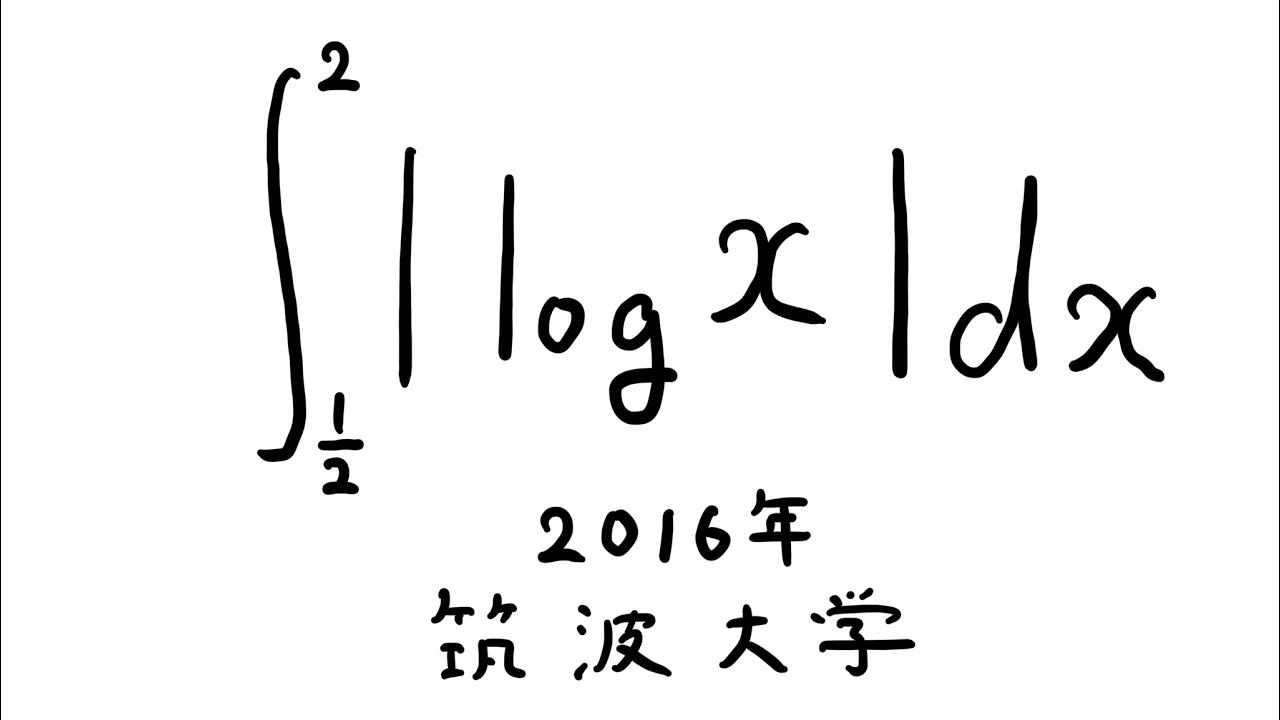問題文全文(内容文):
$\boxed {3} $
平面四辺形$ABCD$において、
$\angle ABC = \dfrac {\pi} {6} , AB = a , BC = b , a \leqq b$とする。
次の条件を満たす長方形$EFGH$を考え、
その面積を$S$とする。
条件:点$A,B,C,D$はそれぞれ
$\quad$辺$EF,FG,GH,HE$上にある。
$\quad$ただし、辺はその両端の点も含むものとする。
(1)$\angle BCG=\theta$とするとき、
$S$を$a,b,\theta$を用いて表せ。
(2)$S$とりうる値の最大値を$a,b$を用いて表せ。
$2025$年東京大学理系過去問題
$\boxed {3} $
平面四辺形$ABCD$において、
$\angle ABC = \dfrac {\pi} {6} , AB = a , BC = b , a \leqq b$とする。
次の条件を満たす長方形$EFGH$を考え、
その面積を$S$とする。
条件:点$A,B,C,D$はそれぞれ
$\quad$辺$EF,FG,GH,HE$上にある。
$\quad$ただし、辺はその両端の点も含むものとする。
(1)$\angle BCG=\theta$とするとき、
$S$を$a,b,\theta$を用いて表せ。
(2)$S$とりうる値の最大値を$a,b$を用いて表せ。
$2025$年東京大学理系過去問題
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed {3} $
平面四辺形$ABCD$において、
$\angle ABC = \dfrac {\pi} {6} , AB = a , BC = b , a \leqq b$とする。
次の条件を満たす長方形$EFGH$を考え、
その面積を$S$とする。
条件:点$A,B,C,D$はそれぞれ
$\quad$辺$EF,FG,GH,HE$上にある。
$\quad$ただし、辺はその両端の点も含むものとする。
(1)$\angle BCG=\theta$とするとき、
$S$を$a,b,\theta$を用いて表せ。
(2)$S$とりうる値の最大値を$a,b$を用いて表せ。
$2025$年東京大学理系過去問題
$\boxed {3} $
平面四辺形$ABCD$において、
$\angle ABC = \dfrac {\pi} {6} , AB = a , BC = b , a \leqq b$とする。
次の条件を満たす長方形$EFGH$を考え、
その面積を$S$とする。
条件:点$A,B,C,D$はそれぞれ
$\quad$辺$EF,FG,GH,HE$上にある。
$\quad$ただし、辺はその両端の点も含むものとする。
(1)$\angle BCG=\theta$とするとき、
$S$を$a,b,\theta$を用いて表せ。
(2)$S$とりうる値の最大値を$a,b$を用いて表せ。
$2025$年東京大学理系過去問題
投稿日:2025.02.27