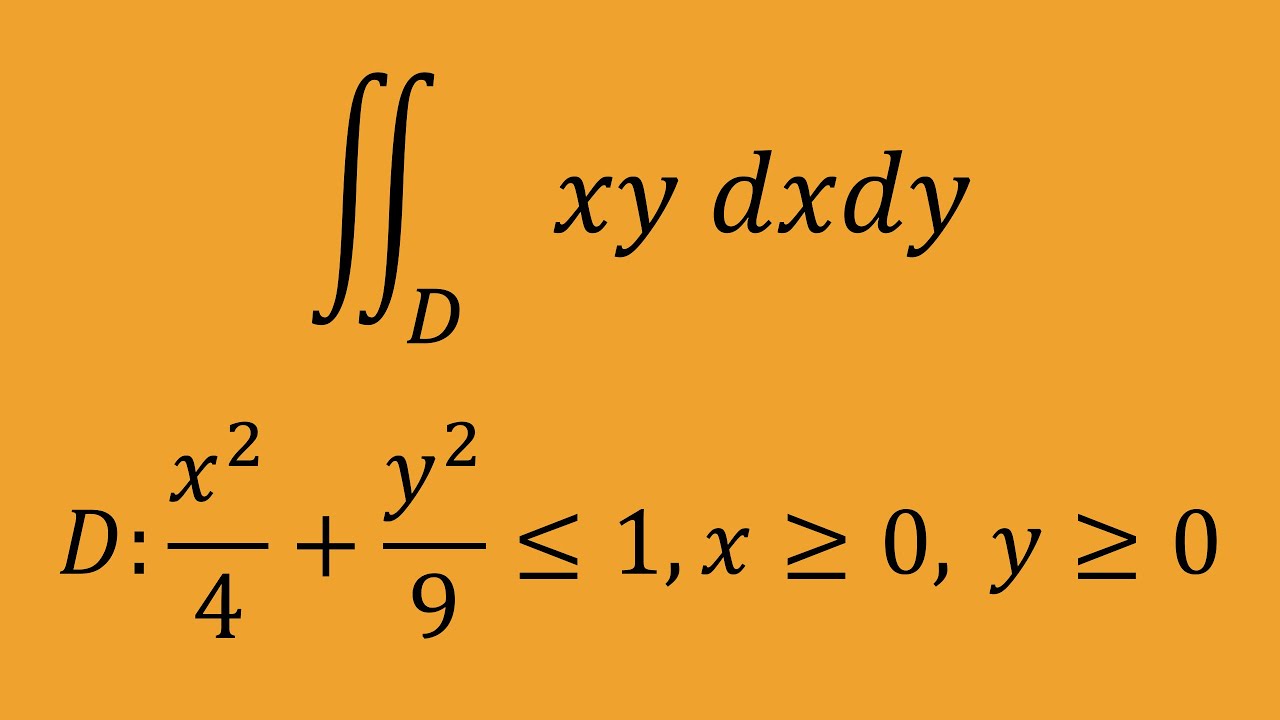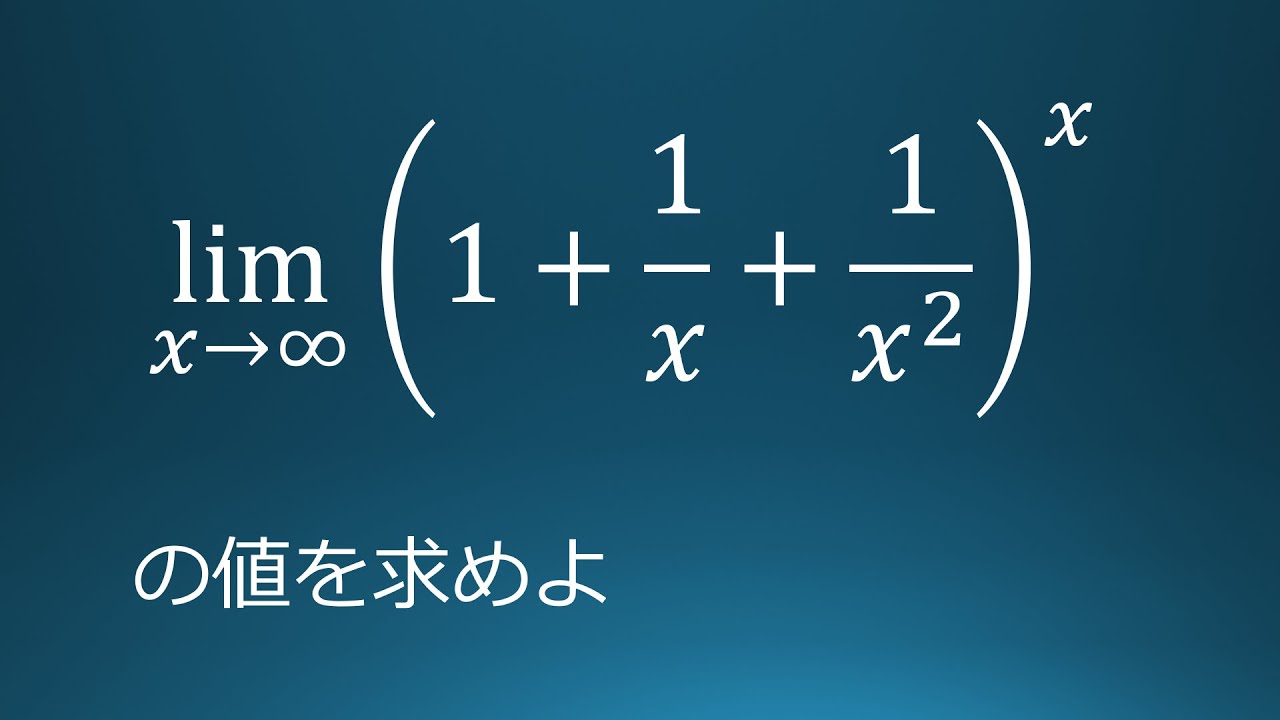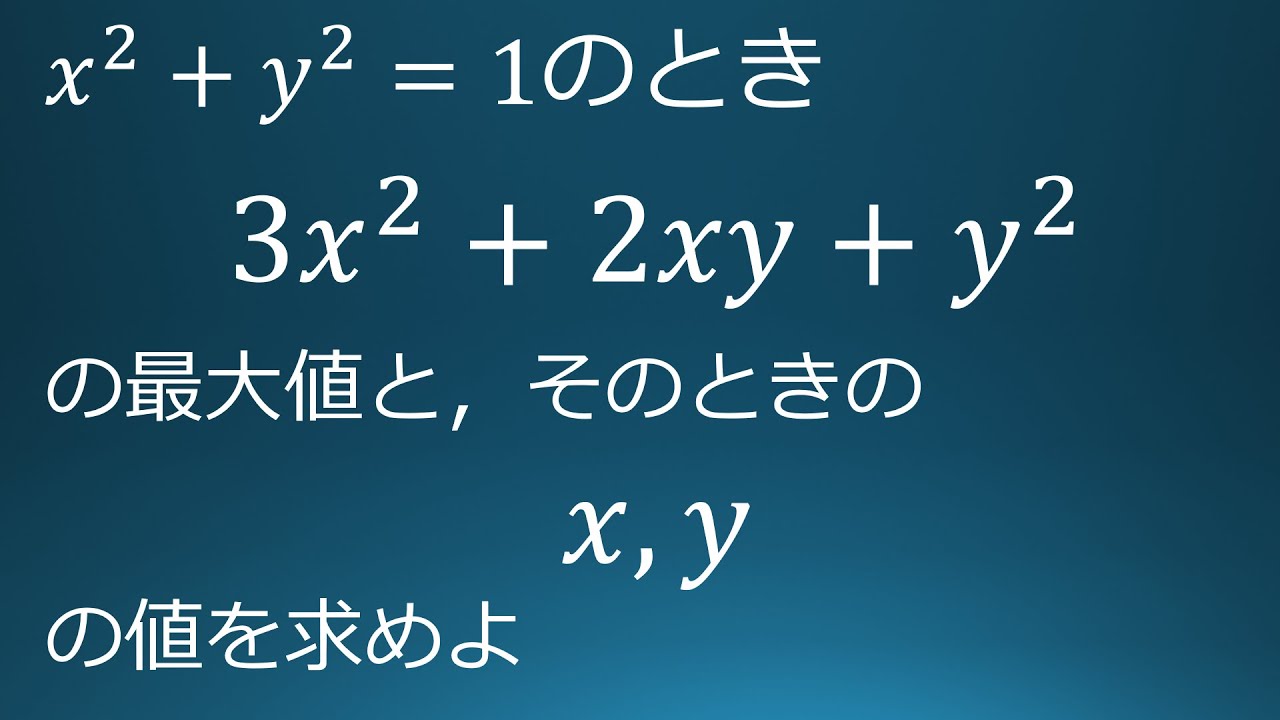問題文全文(内容文):
数学$\textrm{II}$領域(3) 線分と放物線の関係
2点$A(1,\ 1),\ B(3,\ 6)$を結ぶ線分AB
(端点を除く)が放物線$y=x^2+ax+b$
と共有点をもつとき$(a,\ b)$の存在する
領域を図示せよ。
数学$\textrm{II}$領域(3) 線分と放物線の関係
2点$A(1,\ 1),\ B(3,\ 6)$を結ぶ線分AB
(端点を除く)が放物線$y=x^2+ax+b$
と共有点をもつとき$(a,\ b)$の存在する
領域を図示せよ。
単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$領域(3) 線分と放物線の関係
2点$A(1,\ 1),\ B(3,\ 6)$を結ぶ線分AB
(端点を除く)が放物線$y=x^2+ax+b$
と共有点をもつとき$(a,\ b)$の存在する
領域を図示せよ。
数学$\textrm{II}$領域(3) 線分と放物線の関係
2点$A(1,\ 1),\ B(3,\ 6)$を結ぶ線分AB
(端点を除く)が放物線$y=x^2+ax+b$
と共有点をもつとき$(a,\ b)$の存在する
領域を図示せよ。
投稿日:2021.08.20