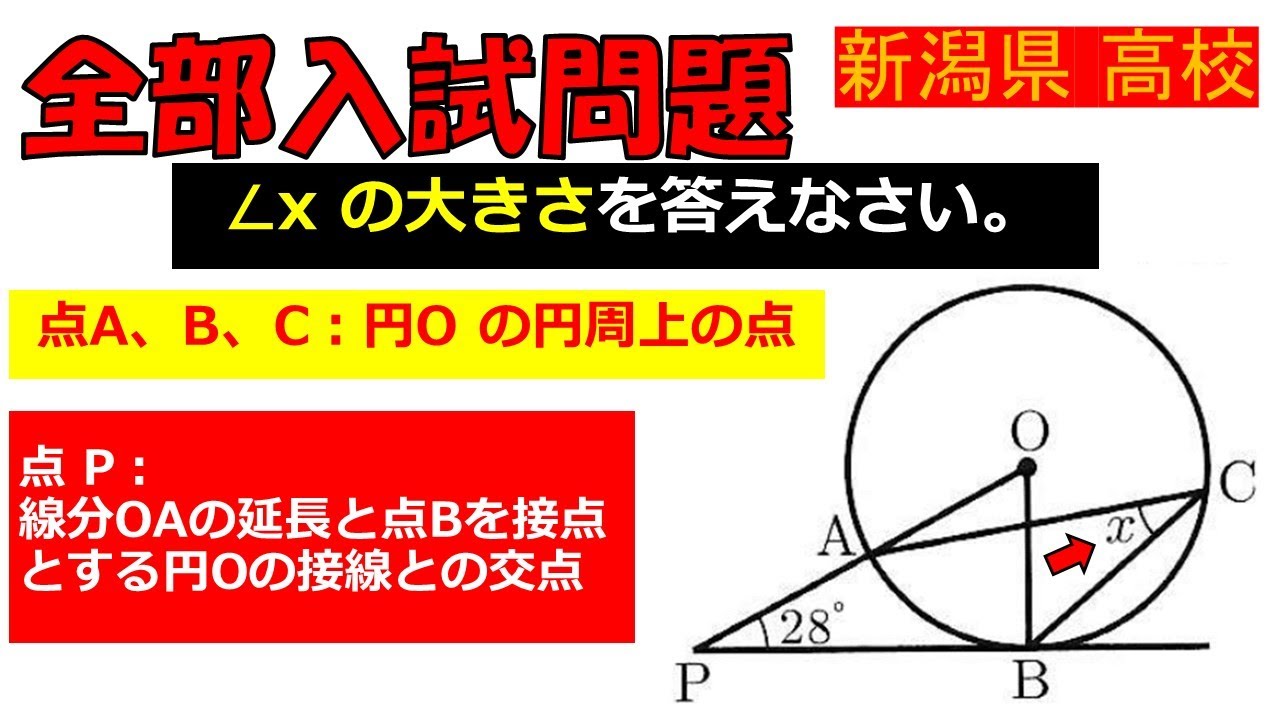
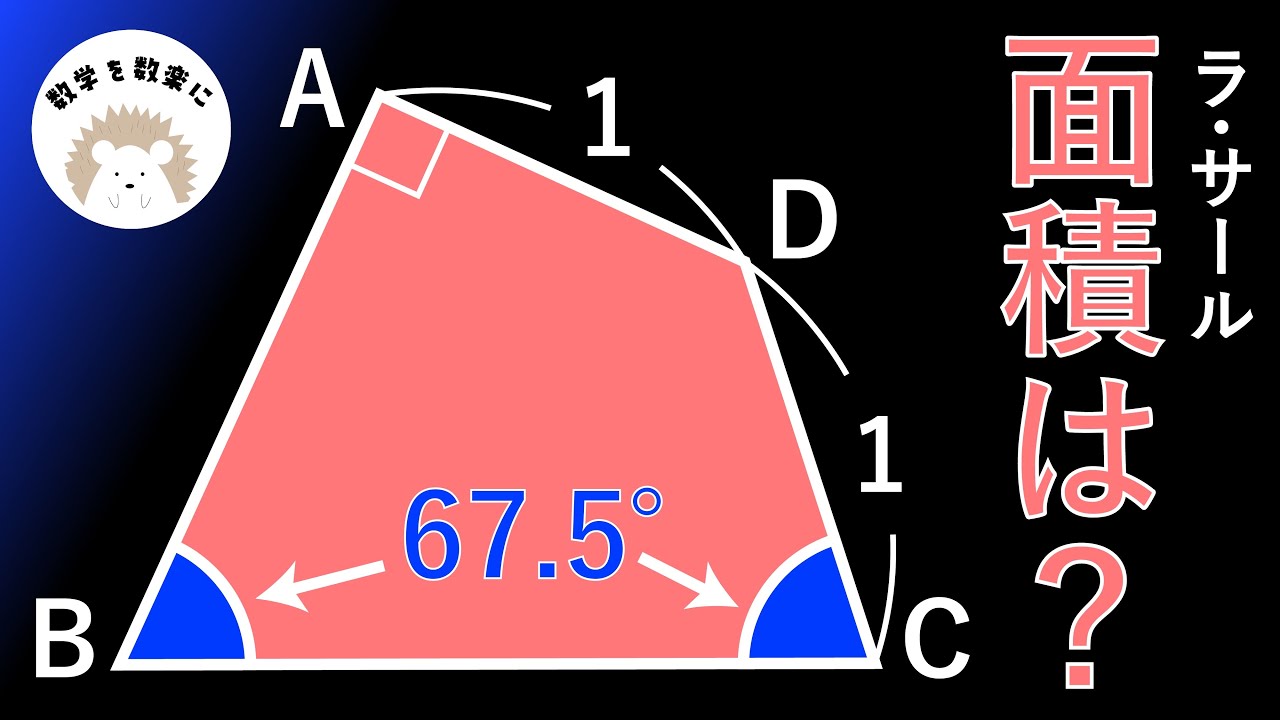
問題文全文(内容文):
1万円以下の税込価格で存在しない価格は何通りか。
税率8%、税抜き価格は自然数。税込み価格は小数点以下は切り捨て
出典:渋谷教育学園幕張高等学校 過去問
1万円以下の税込価格で存在しない価格は何通りか。
税率8%、税抜き価格は自然数。税込み価格は小数点以下は切り捨て
出典:渋谷教育学園幕張高等学校 過去問
単元:
#数学(中学生)#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師:
鈴木貫太郎
問題文全文(内容文):
1万円以下の税込価格で存在しない価格は何通りか。
税率8%、税抜き価格は自然数。税込み価格は小数点以下は切り捨て
出典:渋谷教育学園幕張高等学校 過去問
1万円以下の税込価格で存在しない価格は何通りか。
税率8%、税抜き価格は自然数。税込み価格は小数点以下は切り捨て
出典:渋谷教育学園幕張高等学校 過去問
投稿日:2019.06.11