気付けば一瞬！（慶應中改） - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 中２数学 > 三角形と四角形 > 気付けば一瞬！（慶應中改）

気付けば一瞬！（慶應中改）

問題文全文(内容文)：
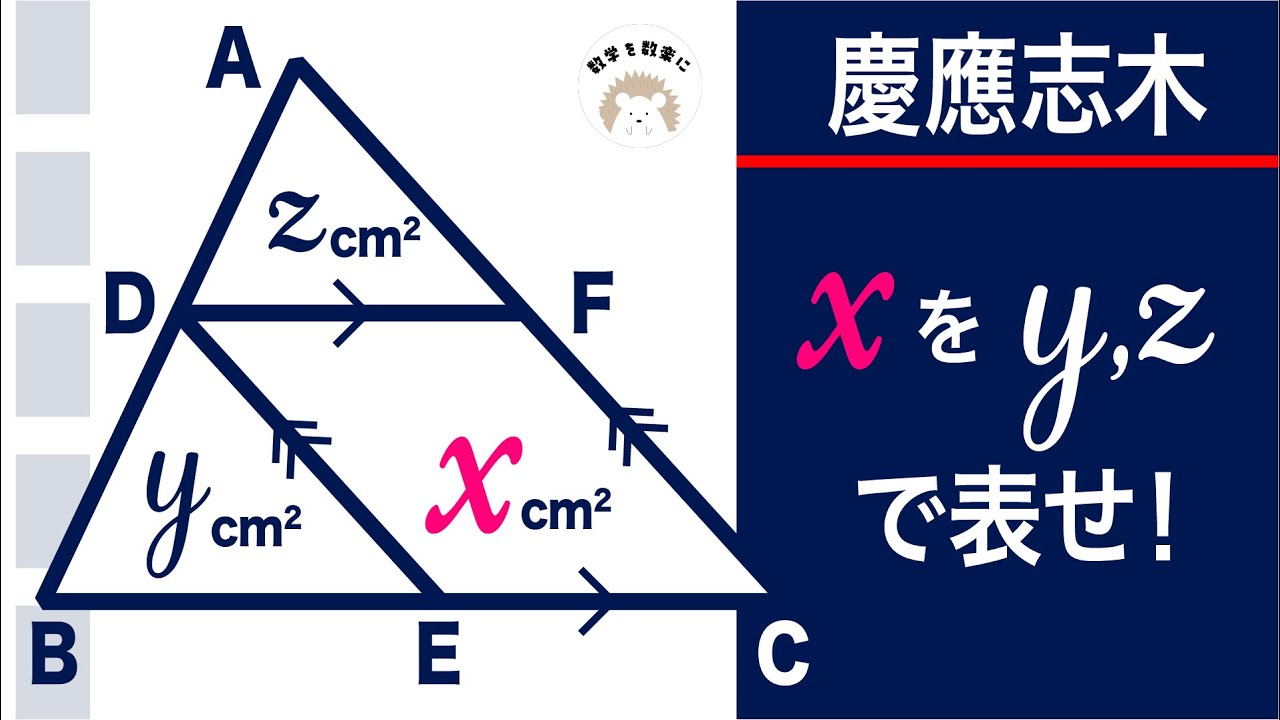
2つの正三角形
△ABC=80㎠
△DEF=?
＊図は動画内参照

慶應義塾中等部
単元： #算数(中学受験)#数学(中学生)#中２数学#過去問解説(学校別)#三角形と四角形
指導講師： 数学を数楽に
問題文全文(内容文)：
2つの正三角形
△ABC=80㎠
△DEF=?
＊図は動画内参照

慶應義塾中等部
投稿日：2022.06.21

＜関連動画＞

報われない時間がある　江戸川学園取手

アイキャッチ画像
単元： #算数(中学受験)#速さ#点の移動・時計算
指導講師： 数学を数楽に
問題文全文(内容文)：
2020年1月1日午前6時から
2020年1月1日午後6時の間に長針と短針は何回重なる？

江戸川学園取手
この動画を見る　

【中学受験問題に挑戦】68　（”大人”は頭の体操）２分した正六角形の面積比

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： 算数・数学ちゃんねる
問題文全文(内容文)：
Aの面積：Bの面積＝？：？
図は動画内参照
この動画を見る　

【小４算数】超使える！折れ線グラフの読み方・書き方！　小４算数基礎講座　第８回

アイキャッチ画像
単元： #算数(中学受験)#表とグラフ#表とグラフ・集合
指導講師： こばちゃん塾
問題文全文(内容文)：
1⃣
①午前11時の気温は何度ですか。
②気温の上がり方がいちばん大きいのは何時から何時までの間ですか。
③気温がいちばん高いのは何時で、それは何度ですか。

2⃣
①午前8時の気温は何度ですか。
②気温がいちばん高いのは何時でそれは何度ですか。
③気温の下がり方がいちばん大きいのは、何時から何時の間ですか。
この動画を見る　

【10秒解説】「正方形一つ分の面積は？」#shorts

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： いつもの先生
問題文全文(内容文)：
正方形一つ分の面積は？

＊図は動画内参照
この動画を見る　

分かるとスッキリする問題

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積#図形の移動
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
分かるとスッキリする問題
この動画を見る　
Back to top