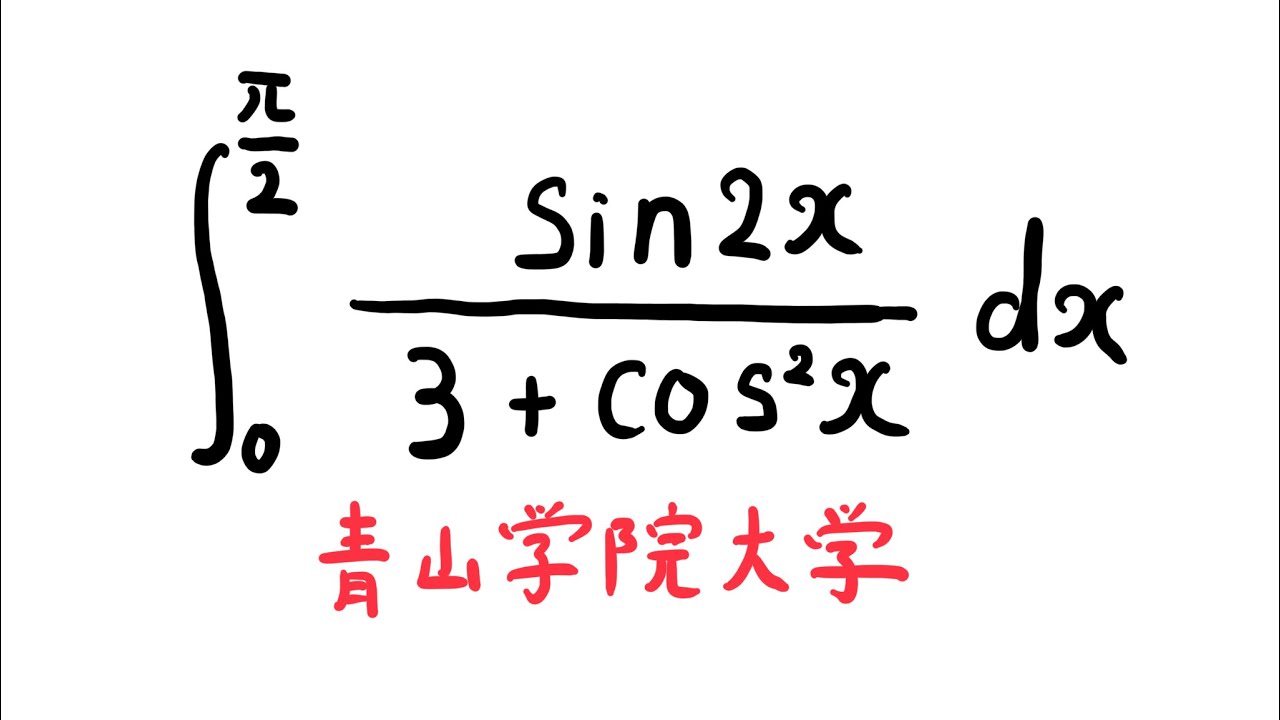問題文全文(内容文):
(1) 0≦a<bとする。関数f(x)を区間a≦x≦bで単調に増加する関数とし、
区間a≦x≦bでf(x)≧0とする。曲線y=f(x)とx軸および2直線x=a,x=bで囲まれた部分を、
y軸の周りに1回転させてできる立体の体積Vは
$V=2\pi\int_a^bxf(x)dx$……①で与えられることを示せ。
(2) (1)の①は、一般の関数f(x) (ただし、a≦x≦bでf(x)≧0)についても成り立つ。
これを利用して、曲線y=-x²+2xとx軸で囲まれた部分を、
y軸の周りに1回転させてできる立体の体積を求めよ。
(1) 0≦a<bとする。関数f(x)を区間a≦x≦bで単調に増加する関数とし、
区間a≦x≦bでf(x)≧0とする。曲線y=f(x)とx軸および2直線x=a,x=bで囲まれた部分を、
y軸の周りに1回転させてできる立体の体積Vは
$V=2\pi\int_a^bxf(x)dx$……①で与えられることを示せ。
(2) (1)の①は、一般の関数f(x) (ただし、a≦x≦bでf(x)≧0)についても成り立つ。
これを利用して、曲線y=-x²+2xとx軸で囲まれた部分を、
y軸の周りに1回転させてできる立体の体積を求めよ。
単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1) 0≦a<bとする。関数f(x)を区間a≦x≦bで単調に増加する関数とし、
区間a≦x≦bでf(x)≧0とする。曲線y=f(x)とx軸および2直線x=a,x=bで囲まれた部分を、
y軸の周りに1回転させてできる立体の体積Vは
$V=2\pi\int_a^bxf(x)dx$……①で与えられることを示せ。
(2) (1)の①は、一般の関数f(x) (ただし、a≦x≦bでf(x)≧0)についても成り立つ。
これを利用して、曲線y=-x²+2xとx軸で囲まれた部分を、
y軸の周りに1回転させてできる立体の体積を求めよ。
(1) 0≦a<bとする。関数f(x)を区間a≦x≦bで単調に増加する関数とし、
区間a≦x≦bでf(x)≧0とする。曲線y=f(x)とx軸および2直線x=a,x=bで囲まれた部分を、
y軸の周りに1回転させてできる立体の体積Vは
$V=2\pi\int_a^bxf(x)dx$……①で与えられることを示せ。
(2) (1)の①は、一般の関数f(x) (ただし、a≦x≦bでf(x)≧0)についても成り立つ。
これを利用して、曲線y=-x²+2xとx軸で囲まれた部分を、
y軸の周りに1回転させてできる立体の体積を求めよ。
投稿日:2025.07.29