【数学】三角形の五心！特徴をまとめてみた（重心編） #Shorts

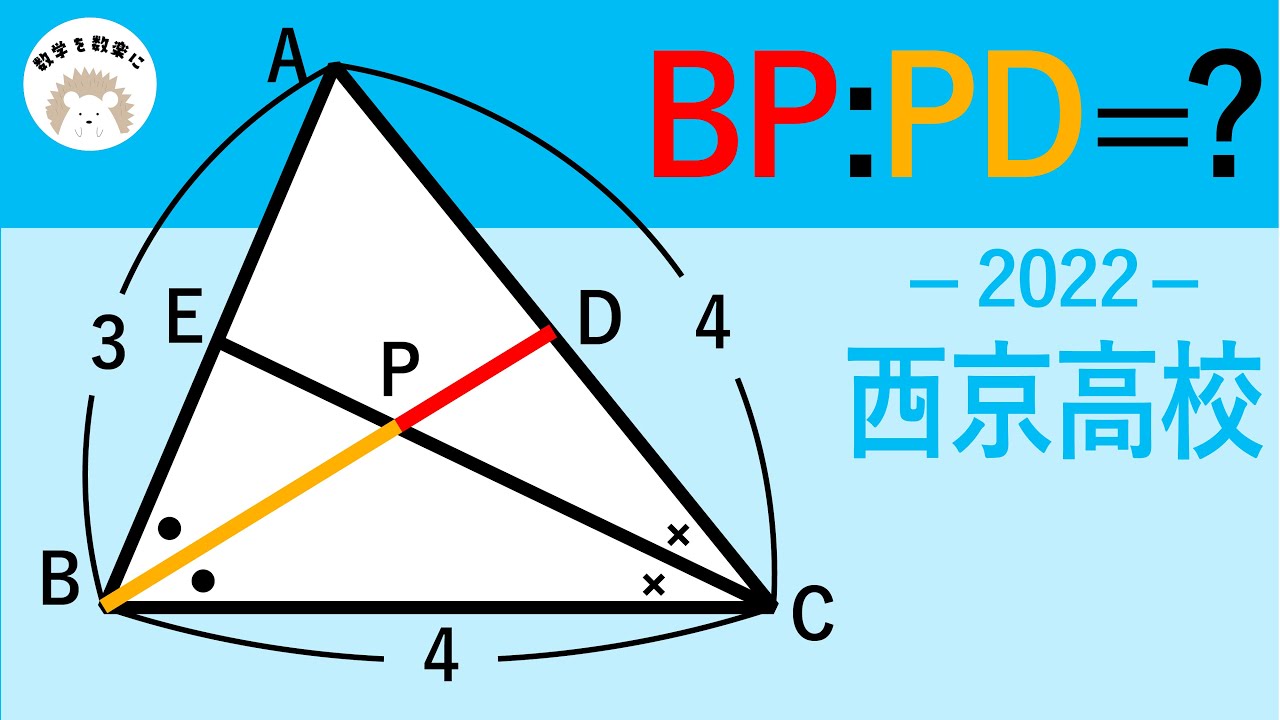
問題文全文(内容文)：
三角形の五心(重心)に関して解説していきます。

単元： #数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)

指導講師：数学・算数の楽しさを思い出した / Ken

問題文全文(内容文)：
三角形の五心(重心)に関して解説していきます。

投稿日：2023.03.04

単元： #数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)

指導講師：【ゼロから理解できる】高校数学・物理

問題文全文(内容文)：
円$x^2+y^2=25$上の点$P(3,-4)$における接線の方程式を求めよ。

この動画を見る　

単元： #数学(中学生)#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#高校入試過去問(数学)#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
BF:FG:FC=?
＊図は動画内参照

智弁学園高等学校

この動画を見る　

単元： #数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)

指導講師：【楽しい授業動画】あきとんとん

この動画を見る　

単元： #数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#立体図形#立体図形その他#高校入試過去問(数学)#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
円錐の底面の半径は？
＊図は動画内参照

2021智辯学園和歌山高等学校（改）

この動画を見る　

単元： #数A#大学入試過去問(数学)#場合の数と確率#確率#漸化式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
同時に1個ずつ取り出して入れかえる.
n回後にAがA,Bである確率を求めよ.

2022一橋大過去問

この動画を見る　