問題文全文(内容文):
メネラウスの定理の証明
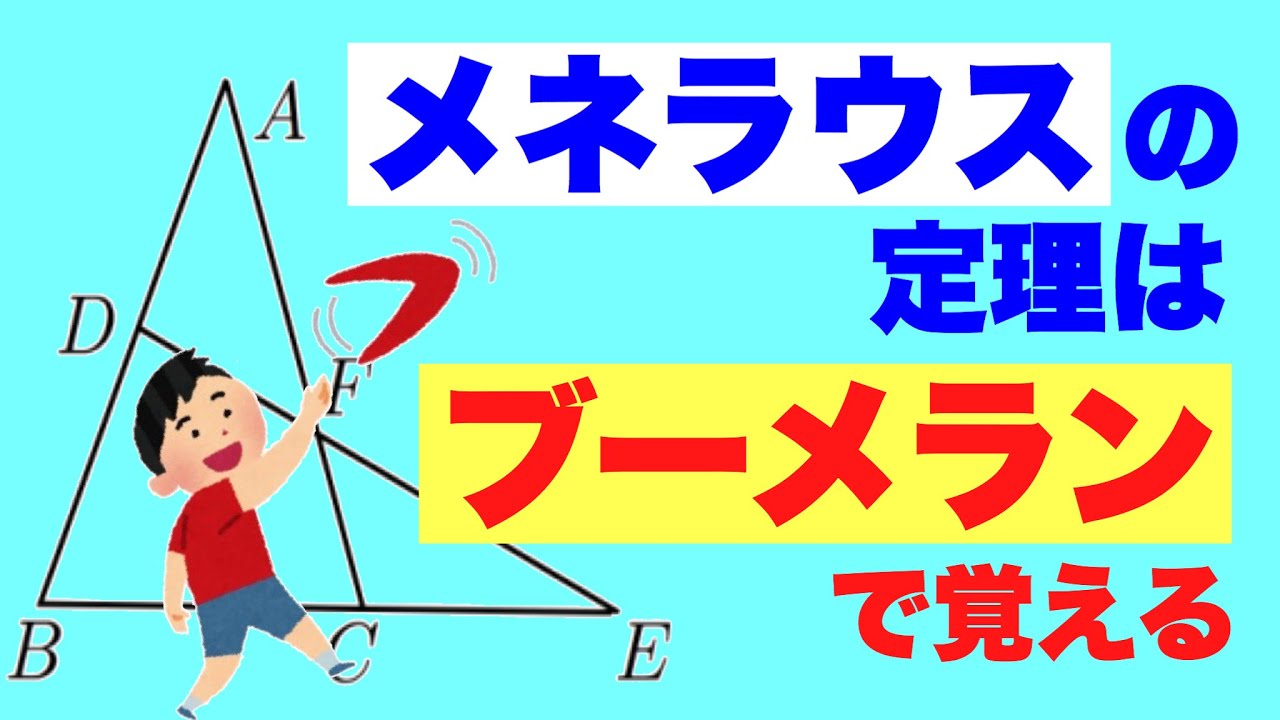
動画内の図で$\displaystyle \frac{a}{b}\times\displaystyle \frac{c}{d}\times\displaystyle \frac{e}{f}$が$1$になることを証明してください。
メネラウスの定理の証明
動画内の図で$\displaystyle \frac{a}{b}\times\displaystyle \frac{c}{d}\times\displaystyle \frac{e}{f}$が$1$になることを証明してください。
単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
メネラウスの定理の証明
動画内の図で$\displaystyle \frac{a}{b}\times\displaystyle \frac{c}{d}\times\displaystyle \frac{e}{f}$が$1$になることを証明してください。
メネラウスの定理の証明
動画内の図で$\displaystyle \frac{a}{b}\times\displaystyle \frac{c}{d}\times\displaystyle \frac{e}{f}$が$1$になることを証明してください。
投稿日:2019.11.02