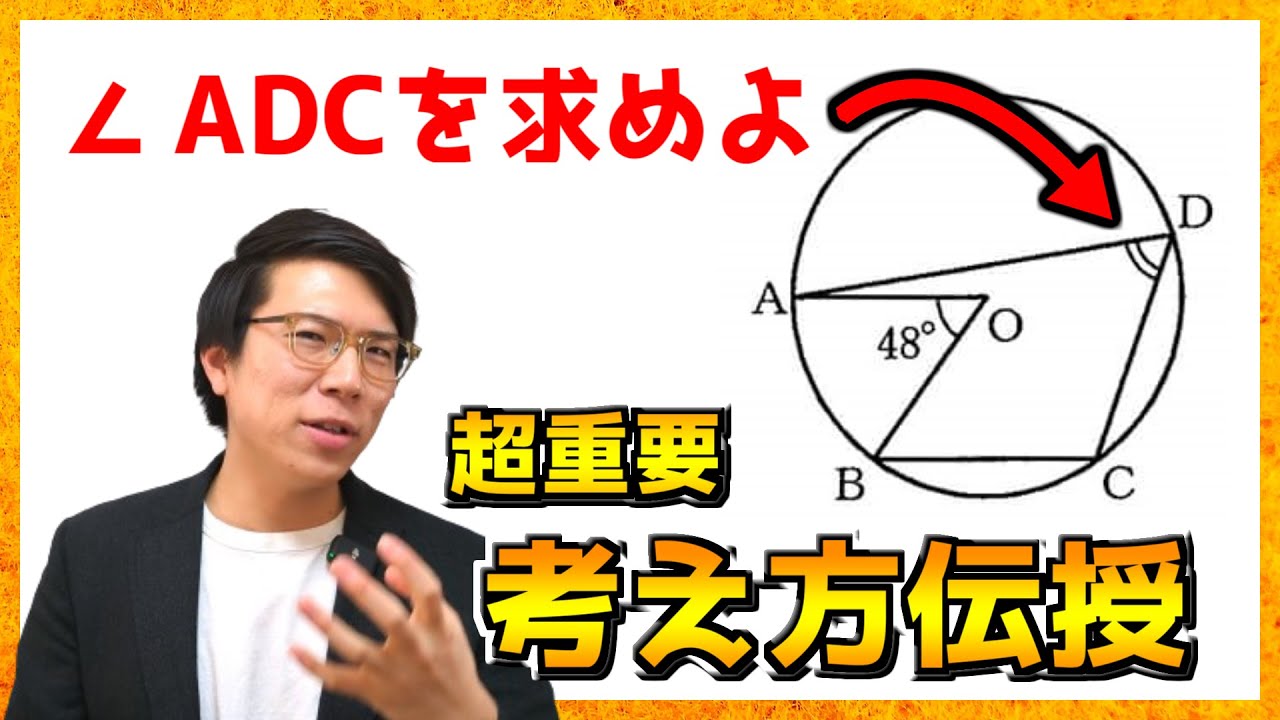
問題文全文(内容文):
三平方の定理を用いて
・一辺の長さしか分かっていない正三角形の面積
・対角線の長さしか分かっていない正方形の面積
を求めます。
三平方の定理を用いて
・一辺の長さしか分かっていない正三角形の面積
・対角線の長さしか分かっていない正方形の面積
を求めます。
チャプター:
0:00 オープニング
0:24 正多角形とは
0:40 正三角形
3:07 正方形
4:19 エンディング
単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
理数個別チャンネル
問題文全文(内容文):
三平方の定理を用いて
・一辺の長さしか分かっていない正三角形の面積
・対角線の長さしか分かっていない正方形の面積
を求めます。
三平方の定理を用いて
・一辺の長さしか分かっていない正三角形の面積
・対角線の長さしか分かっていない正方形の面積
を求めます。
投稿日:2022.03.09