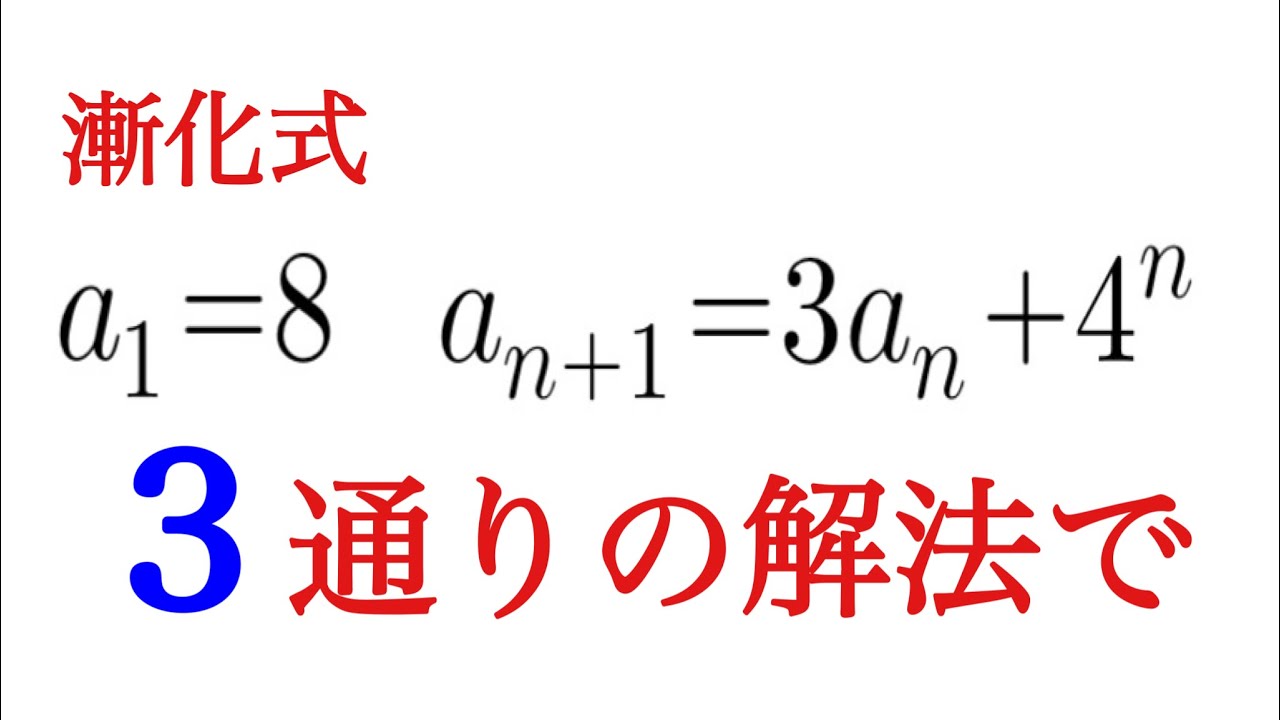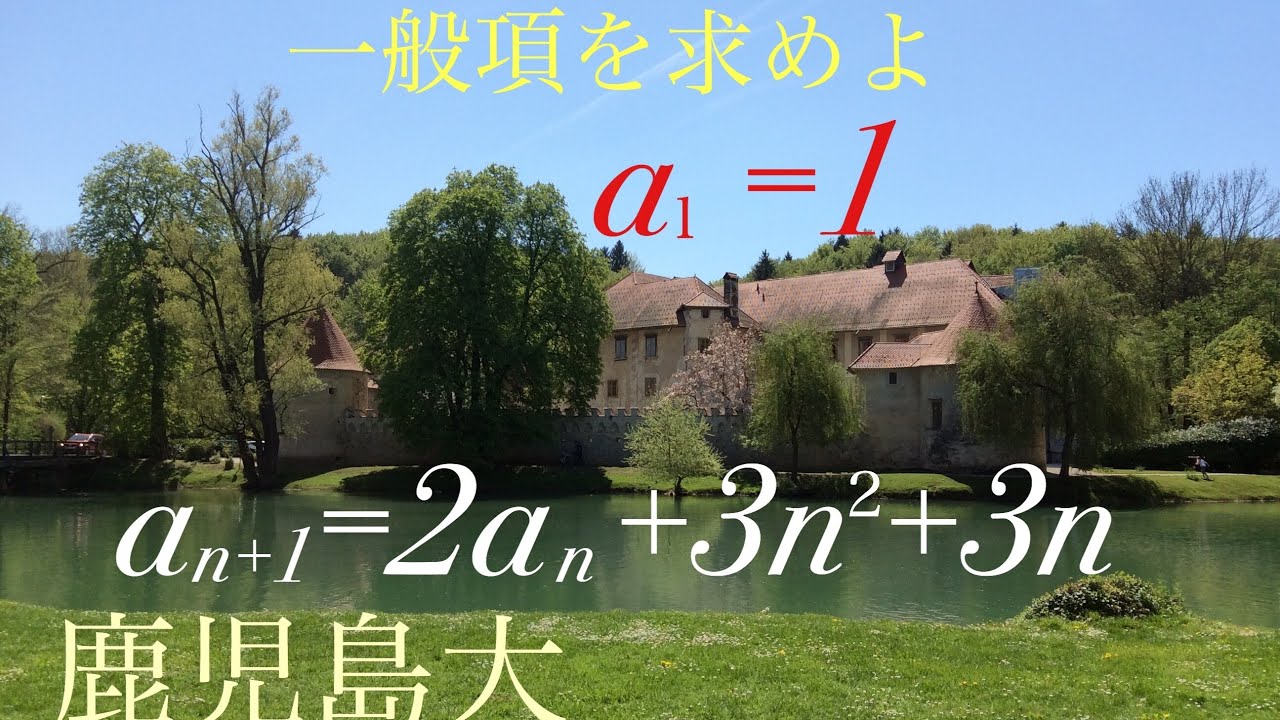問題文全文(内容文):
$\Large\boxed{1}$ (1)$n$を自然数とする。数列$\left\{a_n\right\}$は初項が25, 公差が0でない等差数列であり、3つの項$a_8$, $a_9$, $a_{10}$を
$a_9$, $a_{10}$, $a_8$
の順に並べると等比数列になる。この数列の初項から第$n$項までの和を$S_n$とする。
(i)一般項$a_n$を$n$の式で表すと$a_n$=$\boxed{\ \ ア\ \ }$である。
(ii)不等式$S_n$<0 を満たす最小の$n$の値は$\boxed{\ \ イ\ \ }$である。
$\Large\boxed{1}$ (1)$n$を自然数とする。数列$\left\{a_n\right\}$は初項が25, 公差が0でない等差数列であり、3つの項$a_8$, $a_9$, $a_{10}$を
$a_9$, $a_{10}$, $a_8$
の順に並べると等比数列になる。この数列の初項から第$n$項までの和を$S_n$とする。
(i)一般項$a_n$を$n$の式で表すと$a_n$=$\boxed{\ \ ア\ \ }$である。
(ii)不等式$S_n$<0 を満たす最小の$n$の値は$\boxed{\ \ イ\ \ }$である。
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)$n$を自然数とする。数列$\left\{a_n\right\}$は初項が25, 公差が0でない等差数列であり、3つの項$a_8$, $a_9$, $a_{10}$を
$a_9$, $a_{10}$, $a_8$
の順に並べると等比数列になる。この数列の初項から第$n$項までの和を$S_n$とする。
(i)一般項$a_n$を$n$の式で表すと$a_n$=$\boxed{\ \ ア\ \ }$である。
(ii)不等式$S_n$<0 を満たす最小の$n$の値は$\boxed{\ \ イ\ \ }$である。
$\Large\boxed{1}$ (1)$n$を自然数とする。数列$\left\{a_n\right\}$は初項が25, 公差が0でない等差数列であり、3つの項$a_8$, $a_9$, $a_{10}$を
$a_9$, $a_{10}$, $a_8$
の順に並べると等比数列になる。この数列の初項から第$n$項までの和を$S_n$とする。
(i)一般項$a_n$を$n$の式で表すと$a_n$=$\boxed{\ \ ア\ \ }$である。
(ii)不等式$S_n$<0 を満たす最小の$n$の値は$\boxed{\ \ イ\ \ }$である。
投稿日:2024.03.21