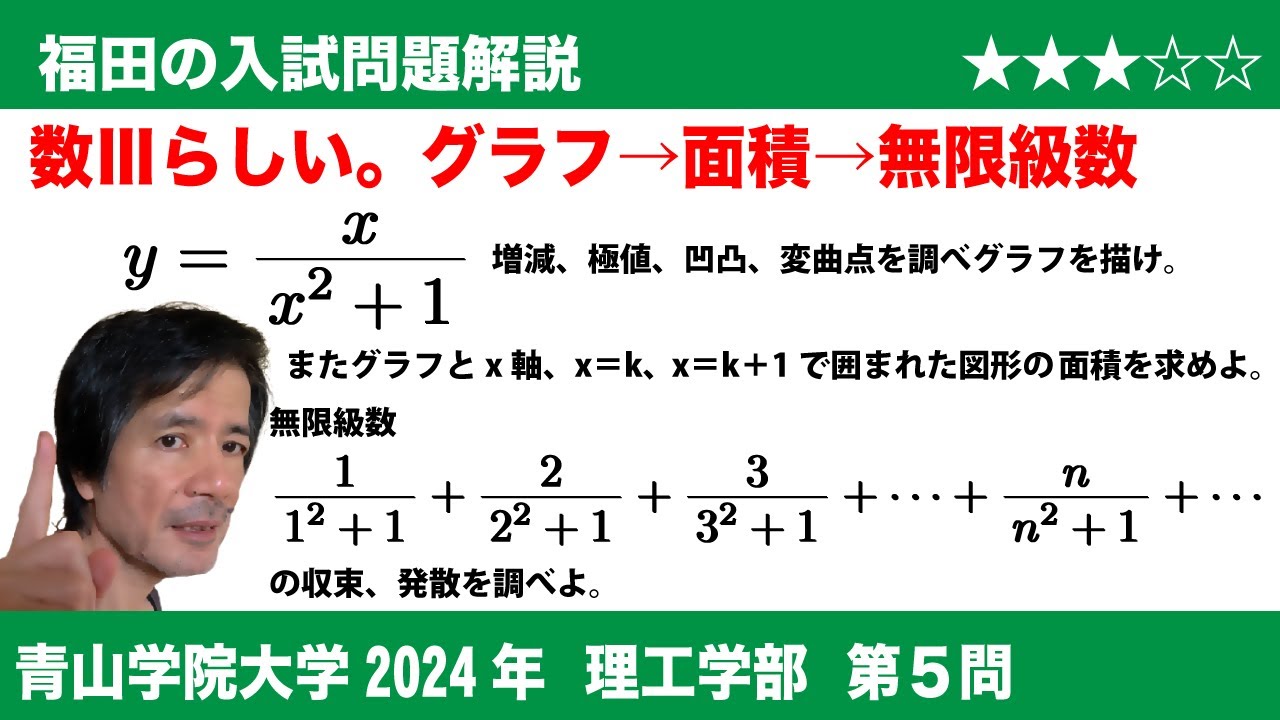
問題文全文(内容文):
無限等比級数の基礎と求め方を解説します。
無限等比級数の基礎と求め方を解説します。
単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
3rd School
問題文全文(内容文):
無限等比級数の基礎と求め方を解説します。
無限等比級数の基礎と求め方を解説します。
投稿日:2023.05.26