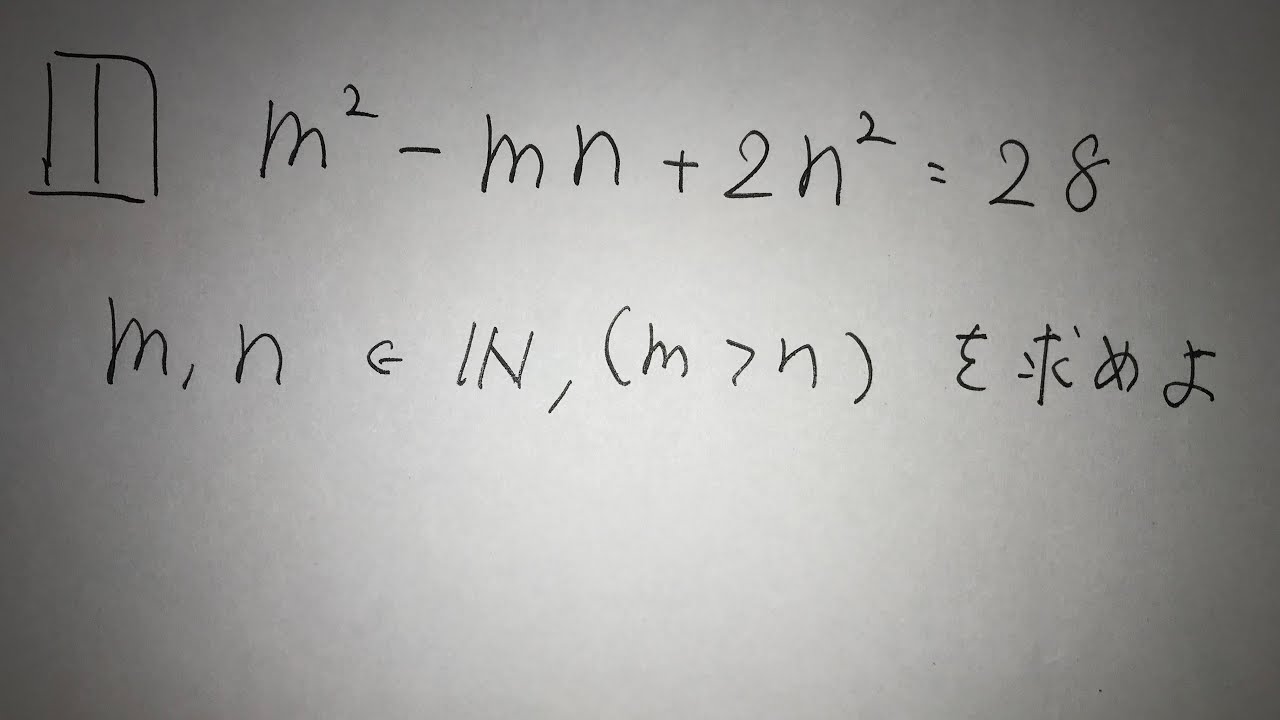問題文全文(内容文):
数列$\left\{a_n\right\}$を次のように定める。
$a_1=1, a_{n+1}=a_n^2+1 (n=1,2,3,\ldots)$
(1)正の整数nが3の倍数のとき、$a_n$は5の倍数となることを示せ。
(2)k,nを正の整数とする。$a_n$が$a_k$の倍数となるための必要十分条件をk,nを
用いて表せ。
(3)$a_{2022}$と$(a_{8091})^2$の最大公約数を求めよ。
2022東京大学理系過去問
数列$\left\{a_n\right\}$を次のように定める。
$a_1=1, a_{n+1}=a_n^2+1 (n=1,2,3,\ldots)$
(1)正の整数nが3の倍数のとき、$a_n$は5の倍数となることを示せ。
(2)k,nを正の整数とする。$a_n$が$a_k$の倍数となるための必要十分条件をk,nを
用いて表せ。
(3)$a_{2022}$と$(a_{8091})^2$の最大公約数を求めよ。
2022東京大学理系過去問
単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数列$\left\{a_n\right\}$を次のように定める。
$a_1=1, a_{n+1}=a_n^2+1 (n=1,2,3,\ldots)$
(1)正の整数nが3の倍数のとき、$a_n$は5の倍数となることを示せ。
(2)k,nを正の整数とする。$a_n$が$a_k$の倍数となるための必要十分条件をk,nを
用いて表せ。
(3)$a_{2022}$と$(a_{8091})^2$の最大公約数を求めよ。
2022東京大学理系過去問
数列$\left\{a_n\right\}$を次のように定める。
$a_1=1, a_{n+1}=a_n^2+1 (n=1,2,3,\ldots)$
(1)正の整数nが3の倍数のとき、$a_n$は5の倍数となることを示せ。
(2)k,nを正の整数とする。$a_n$が$a_k$の倍数となるための必要十分条件をk,nを
用いて表せ。
(3)$a_{2022}$と$(a_{8091})^2$の最大公約数を求めよ。
2022東京大学理系過去問
投稿日:2022.02.26