【数学】中高一貫校問題集2幾何100：円：円周角の定理：作図

問題文全文(内容文)：
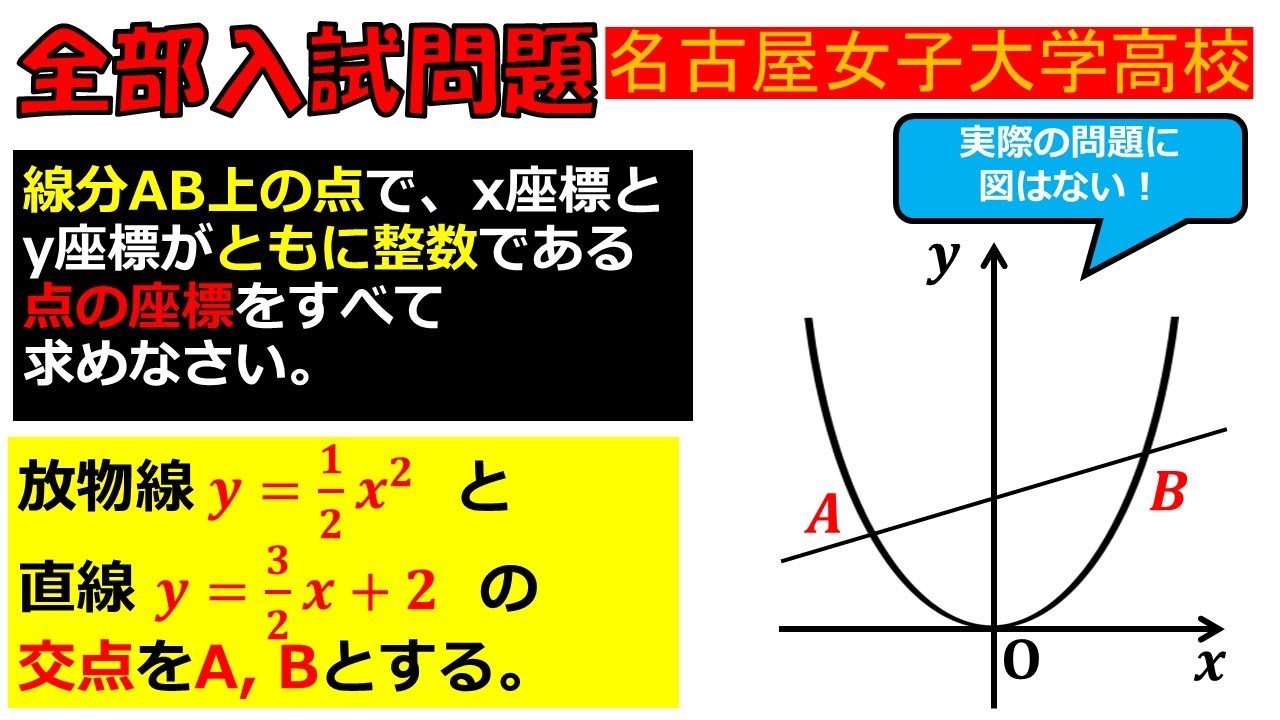
図の△OAは、∠AOB=70°、OA=OBの二等辺三角形である。∠APB=35°となるような△PABを1つ作図しなさい。また、∠APB=35°となる理由を説明しなさい。

チャプター：

0:00 オープニング
0:05 問題文
0:26 解説
1:18 エンディング

単元： #数学(中学生)#中３数学#円

教材： #TK数学#TK数学問題集2(幾何編)#中高教材

指導講師：理数個別チャンネル

投稿日：2023.10.04

単元： #数学(中学生)#中３数学#三平方の定理

教材： #TK数学#TK数学問題集2(幾何編)#中高教材

指導講師：理数個別チャンネル

問題文全文(内容文)：
右の図は、1辺の長さが9cmの正方形ABCDを、頂点Aが辺DC上の点Eに重なるように折り返したもので、PQは折り目の線である。
DE=3cmであるとき、次の問いに答えなさい。
(1)線分APの長さを求めなさい。
(2)線分BQの長さを求めなさい。

この動画を見る　

単元： #数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)

指導講師：数学を数楽に

問題文全文(内容文)：
次の?に当てはまる式を求めよ。
$\frac{a+2}{a+1} -\frac{a+3}{a+2} +\frac{a+4}{a+3} - \frac{a+5}{a+4}
= \frac{?}{(a+1)(a+2)(a+3)(a+4)}$

渋谷教育学園幕張高等学校

この動画を見る　

単元： #数学(中学生)#中３数学#式の計算（展開、因数分解）#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$ \dfrac{10^{2021}+1}{10^{2022}+1}$ VS $ \dfrac{10^{2022}+1}{10^{2023}+1}$
どちらが大きいか?

この動画を見る　

単元： #数学(中学生)#中３数学#式の計算（展開、因数分解）

指導講師：高校入試から見た数学の世界「全部入試問題」by しろたん

問題文全文(内容文)：
$ x=2\sqrt3+2\sqrt2 $
$ y=\sqrt3-\sqrt2 $ のとき

$ x^2-4y^2 $の値を求めよ.

成城学園高校過去問

この動画を見る　

単元： #数学(中学生)#中３数学#三平方の定理

指導講師：理数個別チャンネル

問題文全文(内容文)：
半径6cmの円と半径4cmの円が外接している。これら2つの円に外接して、かつ1つの共通外接線に接する円のうち小さい方の円の半径を求めよう。

この動画を見る　