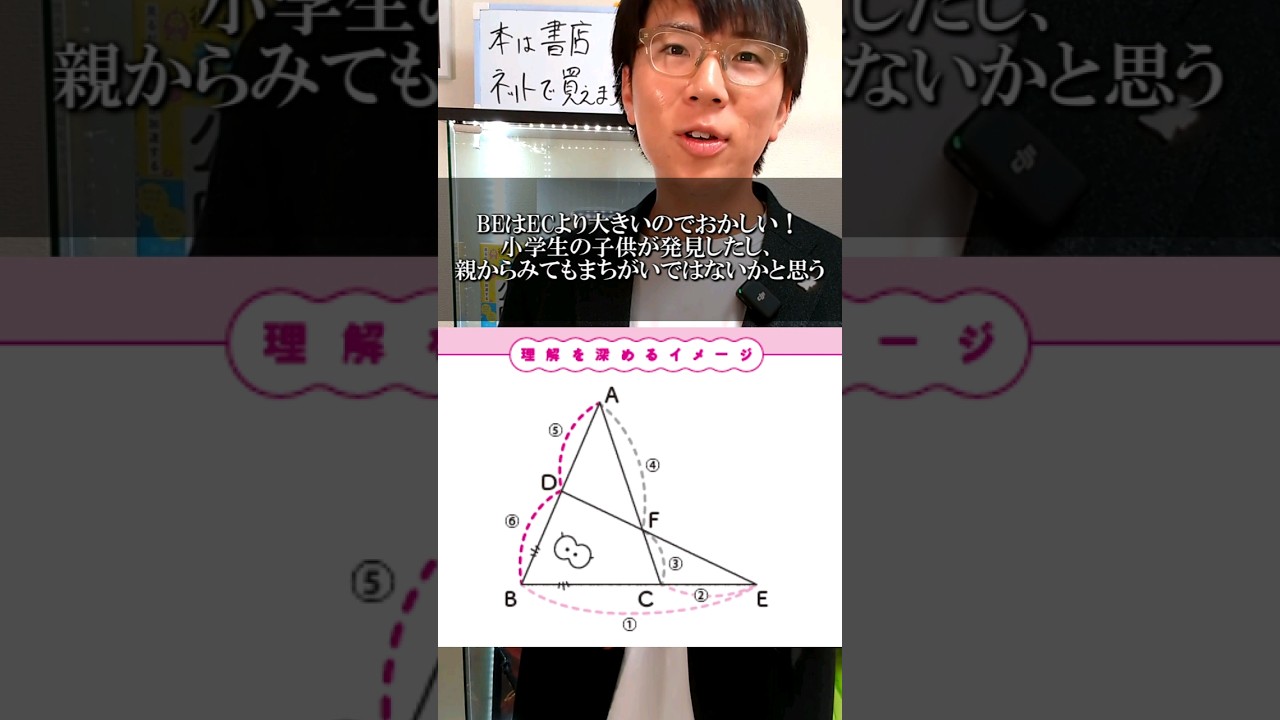
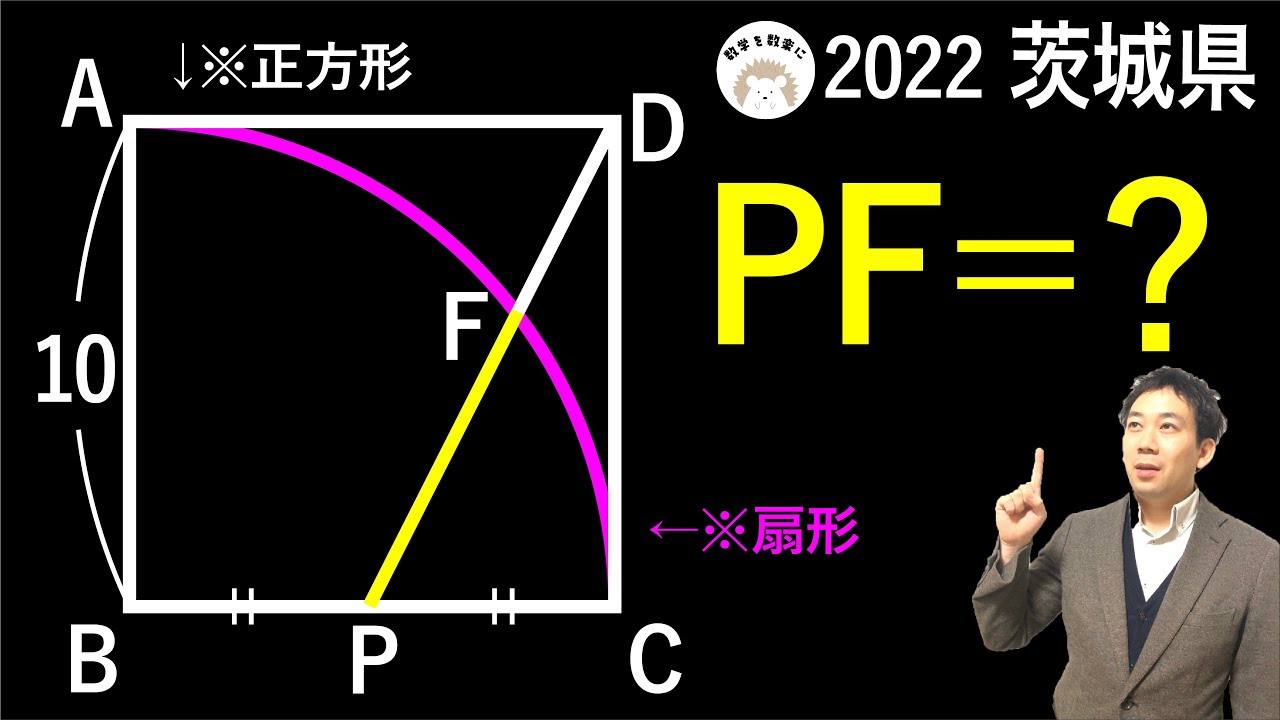
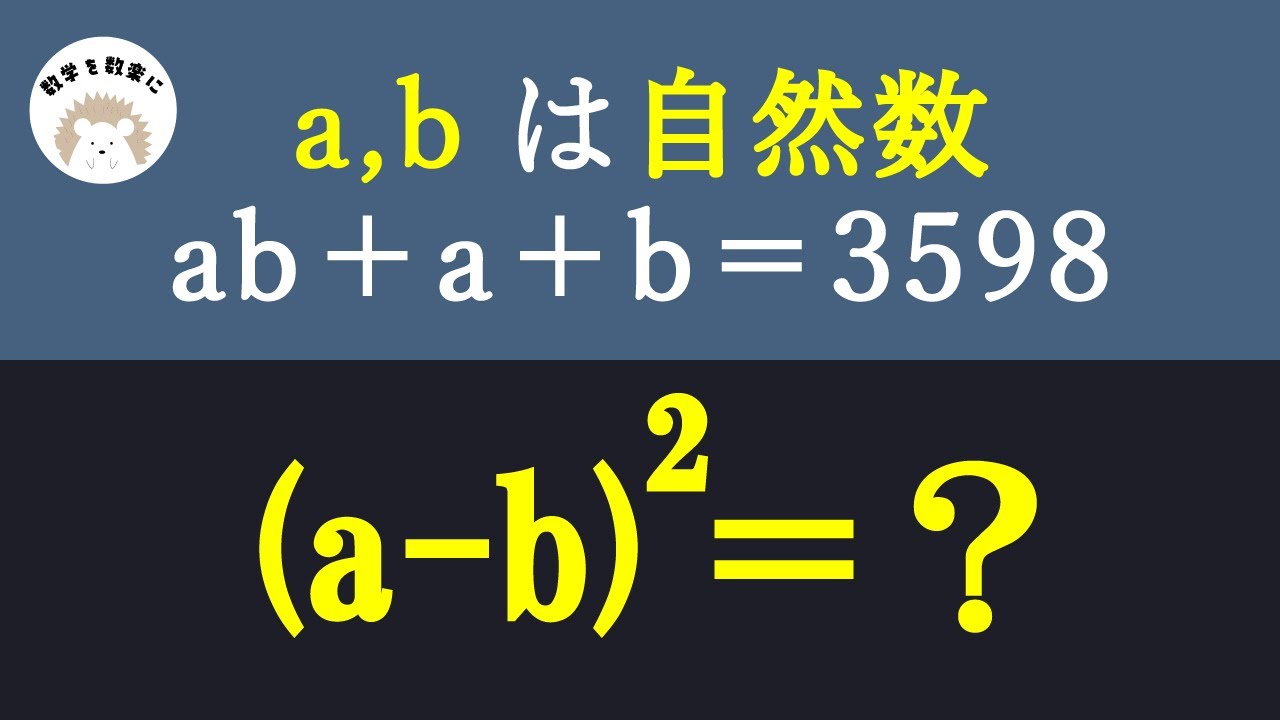問題文全文(内容文)：
動画内手順1の（Step 1）と（Step 4）により、4点C,G,H,[ウ]は同一円周上にあることが分かる。
よって、$\angle CHG =$[エ]である。
一方、点Eは円Oの周上にあることから、[エ]=[オ]がわかる。
よって、$\angle CHG =$[オ]であるので、4点C,G,H,[カ]は同一円周上にある。
この円が点[ウ]を通ることにより、$\angle OEH =$[アイ]$^{ \circ }$を示すことができる。


[ウ]の解答群
⓪B
①D
②F
③O


[エ]の解答群
⓪$\angle AEC$
①$\angle CDF$
②$\angle CGH$
③$\angle CBO$
④$\angle FOG$


[オ]の解答群
⓪$\angle AED$
①$\angle ADE$
②$\angle BOE$
③$\angle DEG$
④$\angle EOH$


[カ]の解答群
⓪A
①D
②E
③F

-----------------
動画内手順2のとき、$\angle PTS =$[キ]である。
円Oの半径が$\sqrt{ 5 }$で、$OT=3 \sqrt{ 6 }$であったとすると、3点O,P,Rを通る円の半径は$\displaystyle \frac{[ク]\sqrt{ [ケ] }}{[コ]}$であり、RT=[サ]である。


[キ]の解答群
⓪$\angle PQS$
①$\angle PST$
②$\angle QPS$
③$\angle QRS$
④$\angle SRT$