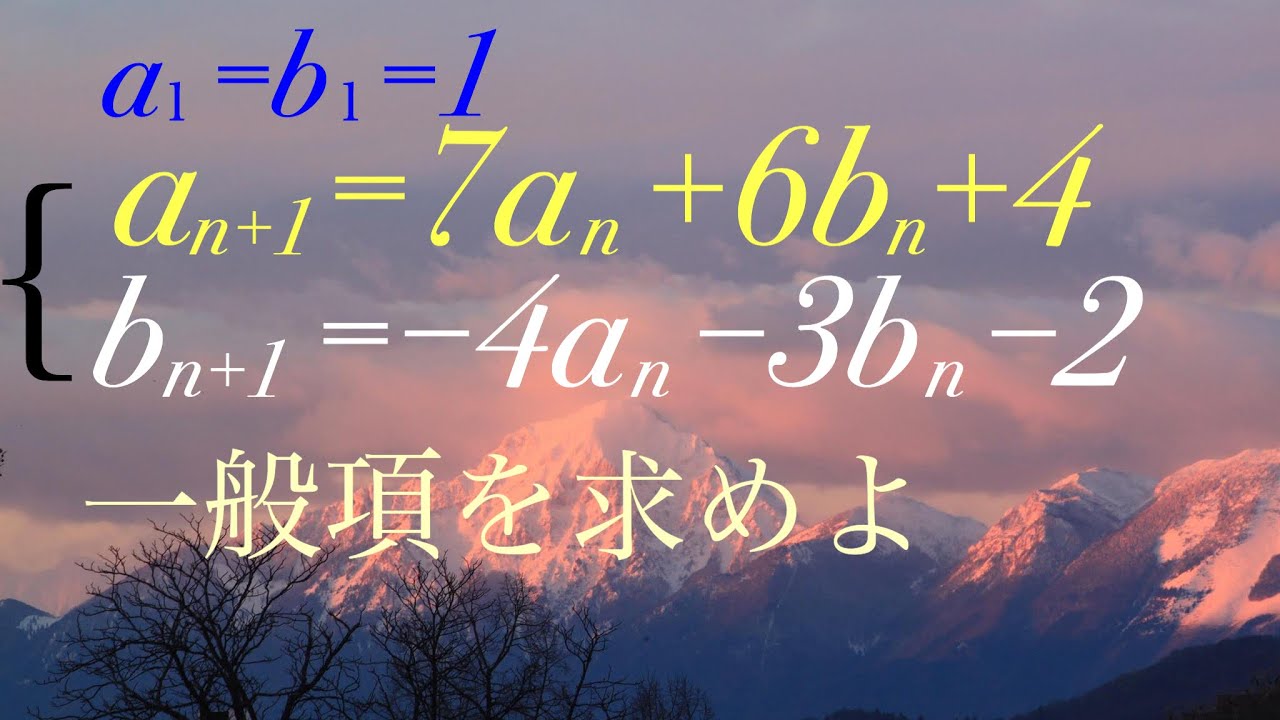問題文全文(内容文):
$\displaystyle \sum_{k=1}^n k^3= \{ \displaystyle \frac{1}{2}n(n+1) \}^2$を示せ。
$\displaystyle \sum_{k=1}^n k^3= \{ \displaystyle \frac{1}{2}n(n+1) \}^2$を示せ。
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
$\displaystyle \sum_{k=1}^n k^3= \{ \displaystyle \frac{1}{2}n(n+1) \}^2$を示せ。
$\displaystyle \sum_{k=1}^n k^3= \{ \displaystyle \frac{1}{2}n(n+1) \}^2$を示せ。
投稿日:2021.01.02