問題文全文(内容文):
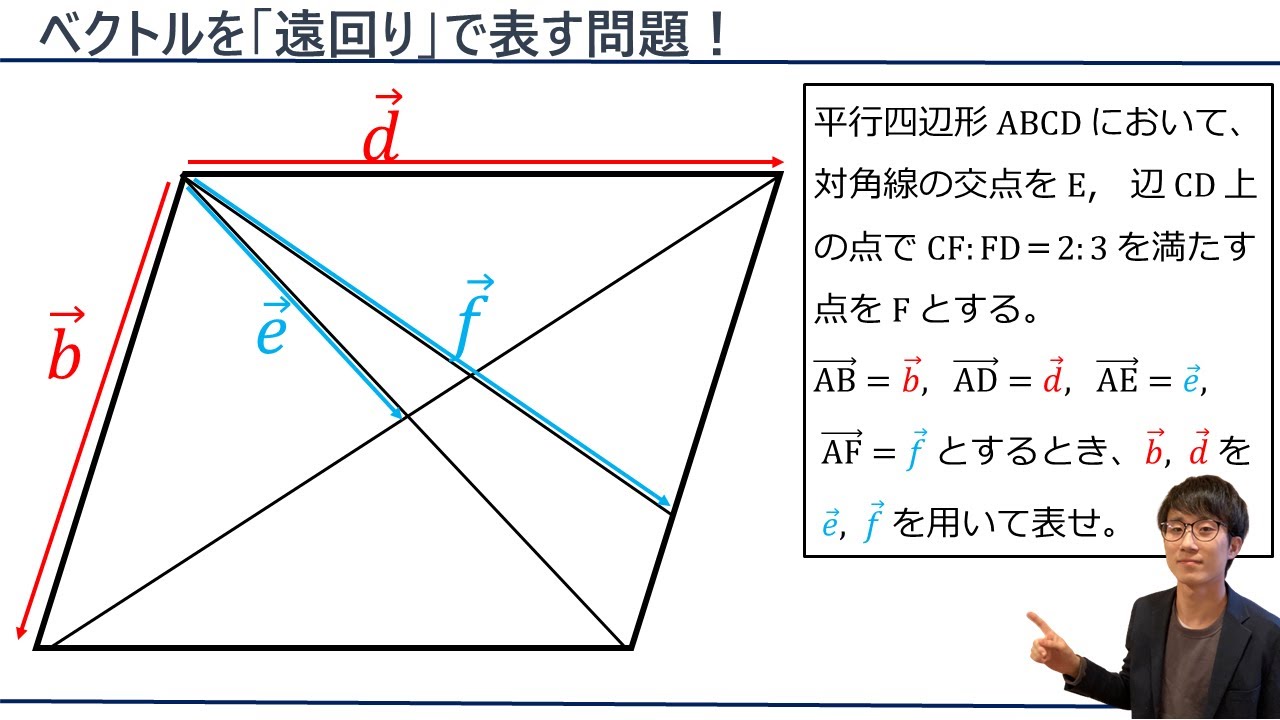
角$A=60°,AB=8,AC=5$である三角形ABCの内心をIとする。$AB=b,AC=c$とするときAIをb,cを用いて表せ.
角$A=60°,AB=8,AC=5$である三角形ABCの内心をIとする。$AB=b,AC=c$とするときAIをb,cを用いて表せ.
チャプター:
0:00 オープニング
0:10 内心の性質
1:13 内角の二等分線の性質
1:48 内心ベクトルを求める
3:51 エンディング
単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
角$A=60°,AB=8,AC=5$である三角形ABCの内心をIとする。$AB=b,AC=c$とするときAIをb,cを用いて表せ.
角$A=60°,AB=8,AC=5$である三角形ABCの内心をIとする。$AB=b,AC=c$とするときAIをb,cを用いて表せ.
投稿日:2022.10.23