問題文全文(内容文):
$\boxed{3}$
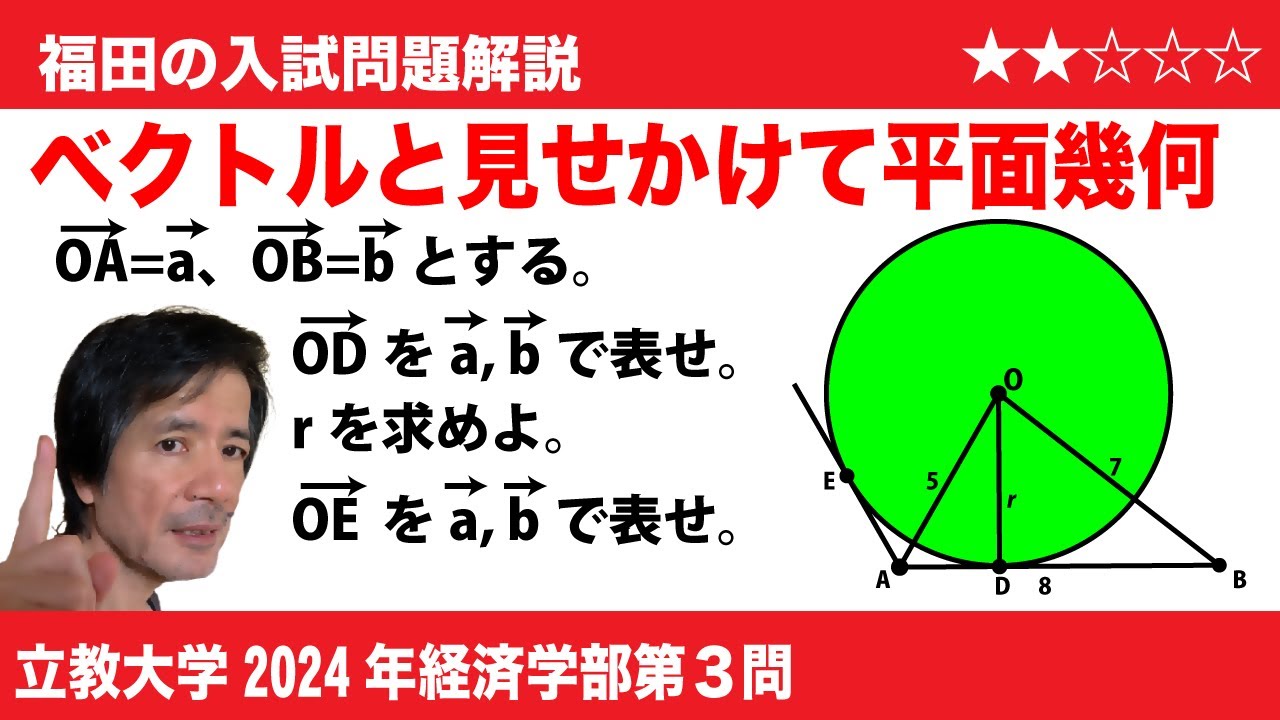
(1)$\triangle ABC$において$AB=6,AC=4,$
$\cos A=\dfrac{1}{4}$とする。
$\triangle ABC$の外心を$H$とし、直線$AH$が
$\triangle ABC$の外接円と交わる点のうち、
点$A$とは異なる点を$P$とする。
このとき、$\overrightarrow{AP}=\dfrac{\boxed{ス}}{\boxed{セ}}\overrightarrow{AB}+\dfrac{\boxed{ソ}}{\boxed{タ}}\overrightarrow{AC}$である。
(2)$\triangle ABC$において$AB=5,AC=6,$
$\cos A=\dfrac{1}{5}$とする。
$\triangle ABC$の内心を$K$とし、
直線$AK$が$\triangle ABC$の内接円と
交わる点のうち、点$A$に近いほうの点を
$Q$とする。
このとき、$\overrightarrow{AQ}=\dfrac{\boxed{チ}-\sqrt{\boxed{ツ}}}{\boxed{テ}}\overrightarrow{AK}$である。
$2025$年早稲田大学人間科学部過去問題
$\boxed{3}$
(1)$\triangle ABC$において$AB=6,AC=4,$
$\cos A=\dfrac{1}{4}$とする。
$\triangle ABC$の外心を$H$とし、直線$AH$が
$\triangle ABC$の外接円と交わる点のうち、
点$A$とは異なる点を$P$とする。
このとき、$\overrightarrow{AP}=\dfrac{\boxed{ス}}{\boxed{セ}}\overrightarrow{AB}+\dfrac{\boxed{ソ}}{\boxed{タ}}\overrightarrow{AC}$である。
(2)$\triangle ABC$において$AB=5,AC=6,$
$\cos A=\dfrac{1}{5}$とする。
$\triangle ABC$の内心を$K$とし、
直線$AK$が$\triangle ABC$の内接円と
交わる点のうち、点$A$に近いほうの点を
$Q$とする。
このとき、$\overrightarrow{AQ}=\dfrac{\boxed{チ}-\sqrt{\boxed{ツ}}}{\boxed{テ}}\overrightarrow{AK}$である。
$2025$年早稲田大学人間科学部過去問題
単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
(1)$\triangle ABC$において$AB=6,AC=4,$
$\cos A=\dfrac{1}{4}$とする。
$\triangle ABC$の外心を$H$とし、直線$AH$が
$\triangle ABC$の外接円と交わる点のうち、
点$A$とは異なる点を$P$とする。
このとき、$\overrightarrow{AP}=\dfrac{\boxed{ス}}{\boxed{セ}}\overrightarrow{AB}+\dfrac{\boxed{ソ}}{\boxed{タ}}\overrightarrow{AC}$である。
(2)$\triangle ABC$において$AB=5,AC=6,$
$\cos A=\dfrac{1}{5}$とする。
$\triangle ABC$の内心を$K$とし、
直線$AK$が$\triangle ABC$の内接円と
交わる点のうち、点$A$に近いほうの点を
$Q$とする。
このとき、$\overrightarrow{AQ}=\dfrac{\boxed{チ}-\sqrt{\boxed{ツ}}}{\boxed{テ}}\overrightarrow{AK}$である。
$2025$年早稲田大学人間科学部過去問題
$\boxed{3}$
(1)$\triangle ABC$において$AB=6,AC=4,$
$\cos A=\dfrac{1}{4}$とする。
$\triangle ABC$の外心を$H$とし、直線$AH$が
$\triangle ABC$の外接円と交わる点のうち、
点$A$とは異なる点を$P$とする。
このとき、$\overrightarrow{AP}=\dfrac{\boxed{ス}}{\boxed{セ}}\overrightarrow{AB}+\dfrac{\boxed{ソ}}{\boxed{タ}}\overrightarrow{AC}$である。
(2)$\triangle ABC$において$AB=5,AC=6,$
$\cos A=\dfrac{1}{5}$とする。
$\triangle ABC$の内心を$K$とし、
直線$AK$が$\triangle ABC$の内接円と
交わる点のうち、点$A$に近いほうの点を
$Q$とする。
このとき、$\overrightarrow{AQ}=\dfrac{\boxed{チ}-\sqrt{\boxed{ツ}}}{\boxed{テ}}\overrightarrow{AK}$である。
$2025$年早稲田大学人間科学部過去問題
投稿日:2025.07.07