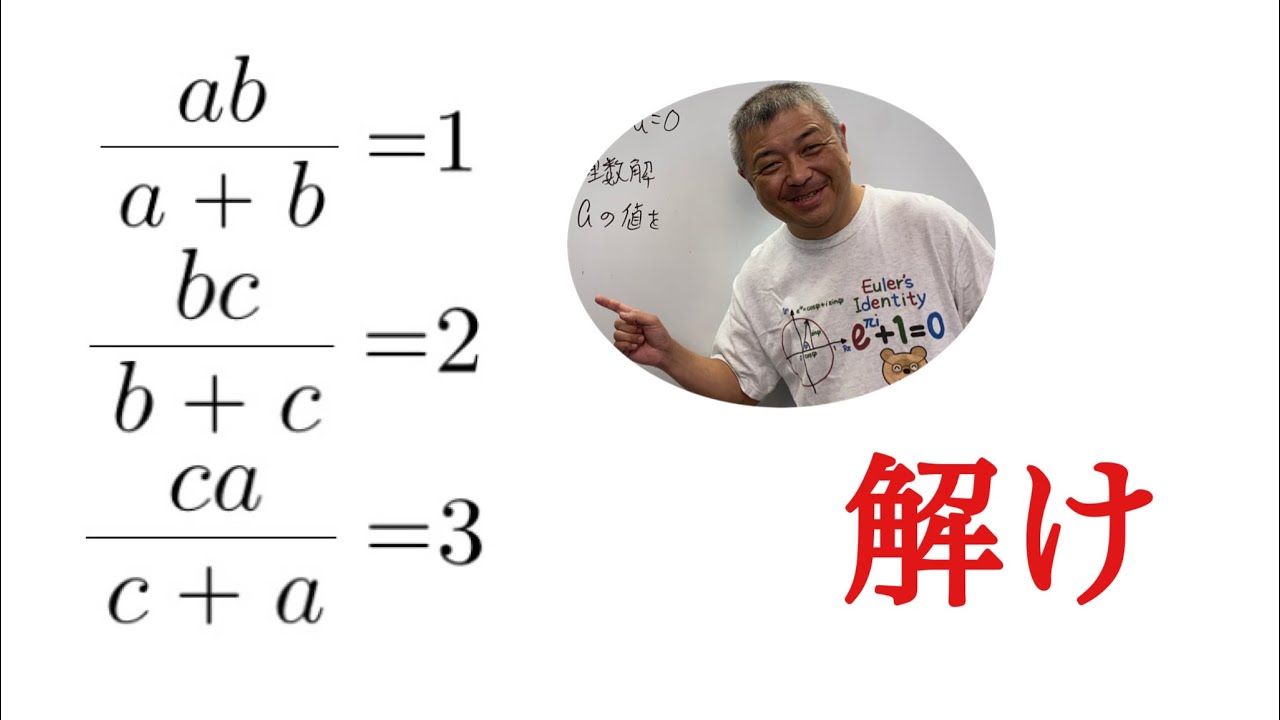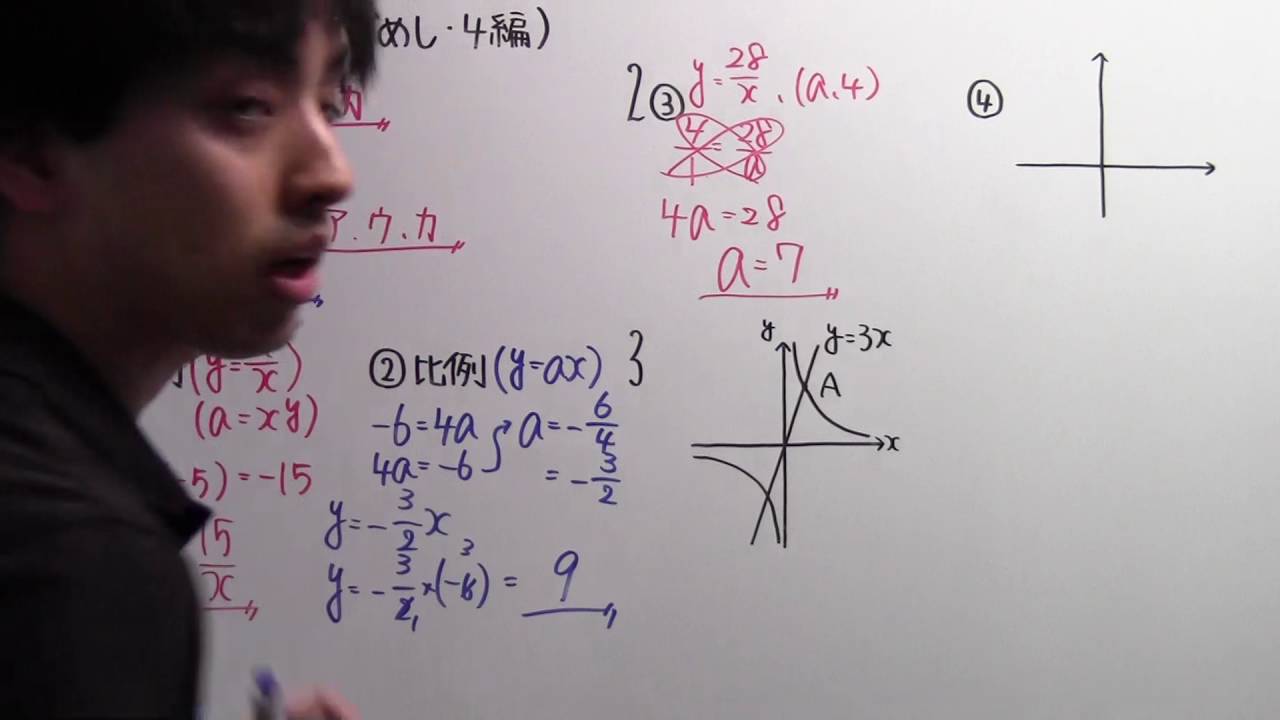問題文全文(内容文):
中2~逆と反例~
「AならはBである」
例題 次のことがらの逆をいいなさい。また、それが正しいかどうか 答えなさい。正しくない場合は、反例を1つ示しなさい。
(1)X=2、y=-3ならばxy=-6である。
(2) 2直線について、ℓ∥mならば、同位角は等しい。
(3) 底辺が6cm、高さが3cmの三角形の面積は9㎠である。
※図は動画内参照
中2~逆と反例~
「AならはBである」
例題 次のことがらの逆をいいなさい。また、それが正しいかどうか 答えなさい。正しくない場合は、反例を1つ示しなさい。
(1)X=2、y=-3ならばxy=-6である。
(2) 2直線について、ℓ∥mならば、同位角は等しい。
(3) 底辺が6cm、高さが3cmの三角形の面積は9㎠である。
※図は動画内参照
単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~逆と反例~
「AならはBである」
例題 次のことがらの逆をいいなさい。また、それが正しいかどうか 答えなさい。正しくない場合は、反例を1つ示しなさい。
(1)X=2、y=-3ならばxy=-6である。
(2) 2直線について、ℓ∥mならば、同位角は等しい。
(3) 底辺が6cm、高さが3cmの三角形の面積は9㎠である。
※図は動画内参照
中2~逆と反例~
「AならはBである」
例題 次のことがらの逆をいいなさい。また、それが正しいかどうか 答えなさい。正しくない場合は、反例を1つ示しなさい。
(1)X=2、y=-3ならばxy=-6である。
(2) 2直線について、ℓ∥mならば、同位角は等しい。
(3) 底辺が6cm、高さが3cmの三角形の面積は9㎠である。
※図は動画内参照
投稿日:2023.03.28