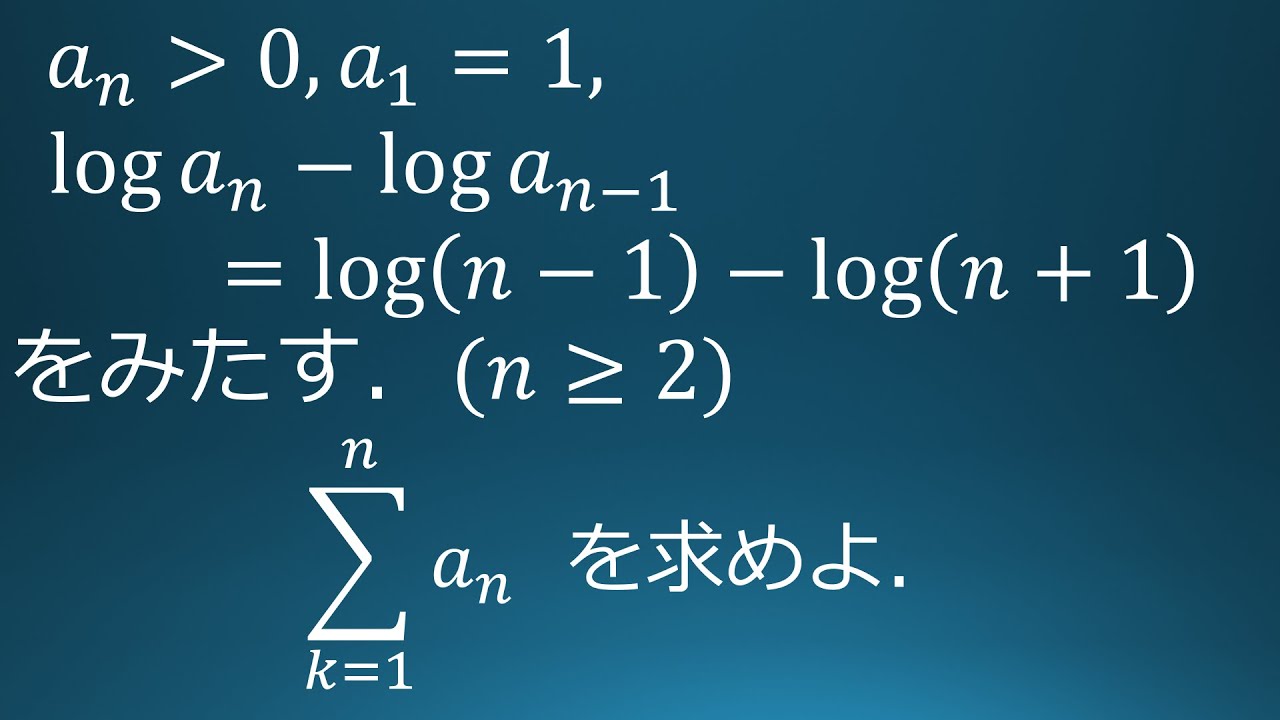問題文全文(内容文):
${\Large\boxed{4}}$
$k$を実数の定数とする。実数$x$は不等式
(*)$2\log_5x-\log_5(6x-5^k) \lt k-1$
を満たすとする。
(1)不等式(*)を満たすxの値の範囲を、$k$を用いて表せ。
(2)$k$を自然数とする。(*)を満たす$x$のうち奇数の個数を$a_k$とし
$S_n=\sum_{k=1}^na_k (n=1,2,3,\ldots)$
とおく。$a_k$を$k$の式で表し、さらに$S_n$を$n$の式で表せ。
(3)(2)の$S_n$に対して、$S_n+n$が10桁の整数となるような自然数$n$
の値を求めよ。なお、必要があれば$0.30 \lt \log_{10}2 \lt 0.31$を用いよ。
2021慶應義塾大学経済学過去問
${\Large\boxed{4}}$
$k$を実数の定数とする。実数$x$は不等式
(*)$2\log_5x-\log_5(6x-5^k) \lt k-1$
を満たすとする。
(1)不等式(*)を満たすxの値の範囲を、$k$を用いて表せ。
(2)$k$を自然数とする。(*)を満たす$x$のうち奇数の個数を$a_k$とし
$S_n=\sum_{k=1}^na_k (n=1,2,3,\ldots)$
とおく。$a_k$を$k$の式で表し、さらに$S_n$を$n$の式で表せ。
(3)(2)の$S_n$に対して、$S_n+n$が10桁の整数となるような自然数$n$
の値を求めよ。なお、必要があれば$0.30 \lt \log_{10}2 \lt 0.31$を用いよ。
2021慶應義塾大学経済学過去問
単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$
$k$を実数の定数とする。実数$x$は不等式
(*)$2\log_5x-\log_5(6x-5^k) \lt k-1$
を満たすとする。
(1)不等式(*)を満たすxの値の範囲を、$k$を用いて表せ。
(2)$k$を自然数とする。(*)を満たす$x$のうち奇数の個数を$a_k$とし
$S_n=\sum_{k=1}^na_k (n=1,2,3,\ldots)$
とおく。$a_k$を$k$の式で表し、さらに$S_n$を$n$の式で表せ。
(3)(2)の$S_n$に対して、$S_n+n$が10桁の整数となるような自然数$n$
の値を求めよ。なお、必要があれば$0.30 \lt \log_{10}2 \lt 0.31$を用いよ。
2021慶應義塾大学経済学過去問
${\Large\boxed{4}}$
$k$を実数の定数とする。実数$x$は不等式
(*)$2\log_5x-\log_5(6x-5^k) \lt k-1$
を満たすとする。
(1)不等式(*)を満たすxの値の範囲を、$k$を用いて表せ。
(2)$k$を自然数とする。(*)を満たす$x$のうち奇数の個数を$a_k$とし
$S_n=\sum_{k=1}^na_k (n=1,2,3,\ldots)$
とおく。$a_k$を$k$の式で表し、さらに$S_n$を$n$の式で表せ。
(3)(2)の$S_n$に対して、$S_n+n$が10桁の整数となるような自然数$n$
の値を求めよ。なお、必要があれば$0.30 \lt \log_{10}2 \lt 0.31$を用いよ。
2021慶應義塾大学経済学過去問
投稿日:2021.07.08