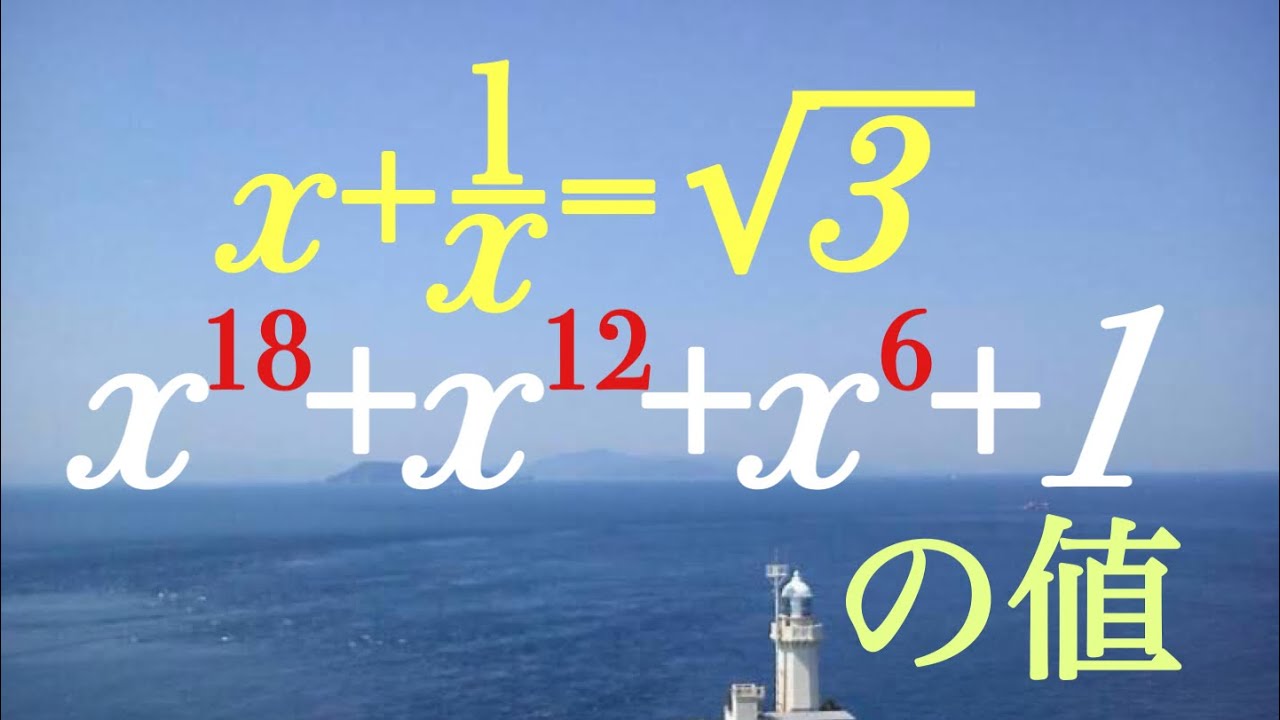一橋大 4次関数と接線・共有点 Mathematics Japanese university entrance exam - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数Ⅱ > 微分法と積分法 > 一橋大　4次関数と接線・共有点 Mathematics Japanese university entrance exam

一橋大　4次関数と接線・共有点 Mathematics Japanese university entrance exam

問題文全文(内容文)：
$f(x)=x^4+x^3+ax^2$と直線$l$との共有点は2個で、$l$はそのうちの一方のみで$f(x)$に接している。
このような直線が存在する$a$の範囲は？

出典：1996年一橋大学　過去問
単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師： 鈴木貫太郎
問題文全文(内容文)：
$f(x)=x^4+x^3+ax^2$と直線$l$との共有点は2個で、$l$はそのうちの一方のみで$f(x)$に接している。
このような直線が存在する$a$の範囲は？

出典：1996年一橋大学　過去問
投稿日：2019.03.07

＜関連動画＞

【数Ⅱ】【微分法と積分法】面積からの定数決定 ※問題文は概要欄

アイキャッチ画像
単元： #数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師： 理数個別チャンネル
問題文全文(内容文)：
放物線$y=ax-x^2~(a > 0)$と$x$軸で囲まれた図形の面積が$\dfrac92$になるように、定数$a$の値を求めよ。
この動画を見る　

聖マリアンナ医大　Σ４乗以上の公式証明

アイキャッチ画像
単元： #数Ⅱ#式と証明#数学(高校生)
指導講師： 鈴木貫太郎
問題文全文(内容文)：
①$\displaystyle \sum_{k=1}^{n}k^3=\left[\dfrac{n(n+1)}{2}\right]$を示せ.
②$(k+1)^5-k^5=5k^4+10k^3+10k^2+5k+1$を利用して
　$\displaystyle \sum_{k=1}^{n}k^4$は$n$の5次式で表せることを示せ.
③$\displaystyle \sum_{k=1}^n k^d$は$n$の$(d+1)$次式で表せることを示せ.

2019聖マリアンナ医大過去問
この動画を見る　

九州大　COS7.5°　複素数

アイキャッチ画像
単元： #数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師： 鈴木貫太郎
問題文全文(内容文)：
$z_1=\displaystyle \frac{1+i}{\sqrt{ 2 }},z_2=\displaystyle \frac{\sqrt{ 3 }+i}{2}$

（1）
$|z_1+z_2|$の値を求めよ

（2）
$\cos 7.5^{ \circ }$を求めよ

出典：1972年九州大学　過去問
この動画を見る　

【高校数学】数Ⅲ-96 三角関数の導関数①

アイキャッチ画像
単元： #数Ⅱ#三角関数#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
$(\sin x)'= ①$

$(\cos x)'= ②$

$(\tan x)'= ③$

次の関数を微分せよ。

④$y=\sin 2x$

⑤$y=\cos (3x+2)$

⑥$y=\tan^2 x$

⑦$y=x \cos x$

⑧$y=\sin(x^2+3)$

⑨$y=\cos\dfrac{1}{x}$
この動画を見る　

山口東京理科大　円の方程式　軌跡

アイキャッチ画像
単元： #数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師： 鈴木貫太郎
問題文全文(内容文)：
点$(s,t)$が$x^2+y^2=\displaystyle \frac{1}{2}$の上を動くとき、$(s+t,st)$を座標とする点の軌跡を図示せよ

出典：山口東京理科大学　過去問
この動画を見る　
PAGE TOP