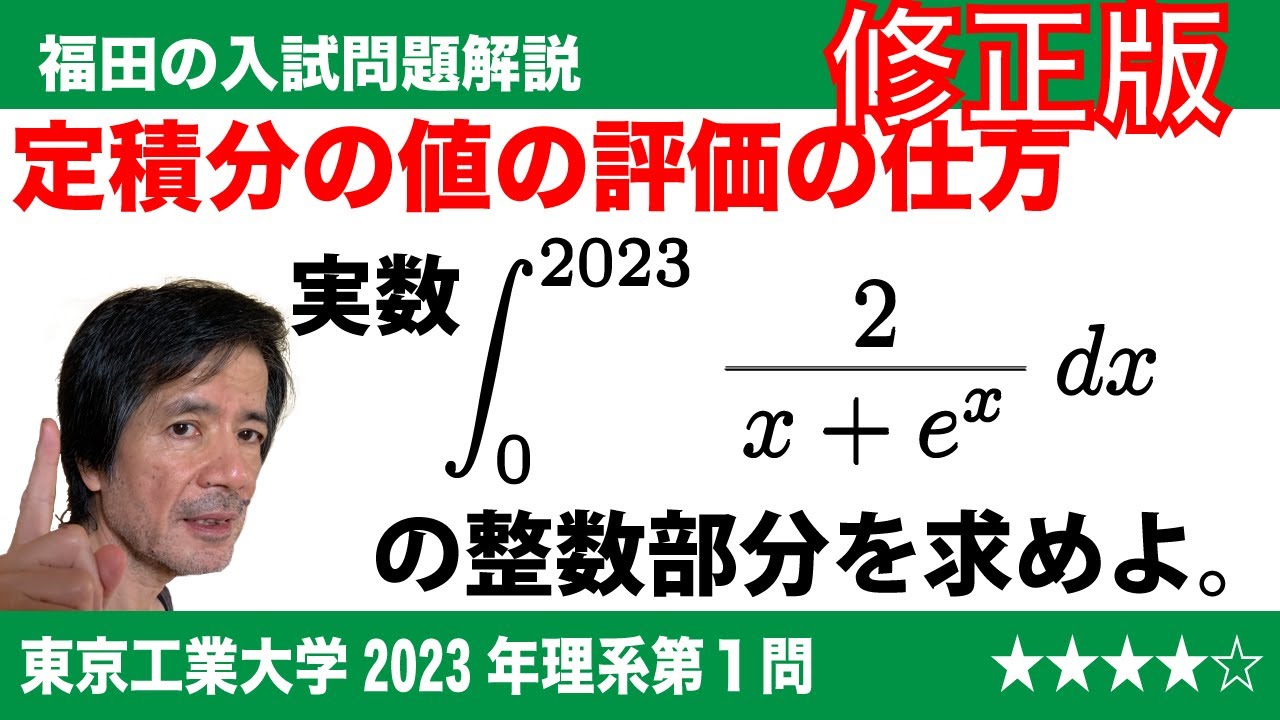
問題文全文(内容文):
半径がaである円Oの直径ABの両端AおよびBから出発して円Oの周上を同じ向きにそれぞれ一定の速さで動く2点P,Qがある。Pの速さはQの速さの2倍で、PがAからBまで動くとき、△APQの面積の最大値を求めよ。また,その時の∠BOQの大きさを求めよ。
半径がaである円Oの直径ABの両端AおよびBから出発して円Oの周上を同じ向きにそれぞれ一定の速さで動く2点P,Qがある。Pの速さはQの速さの2倍で、PがAからBまで動くとき、△APQの面積の最大値を求めよ。また,その時の∠BOQの大きさを求めよ。
チャプター:
0:00 オープニング、問題概要
0:45 微分を使わず、幾何的な思考で解く方法
2:51 微分を使った想定解
5:35 sinの角度変換
単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
半径がaである円Oの直径ABの両端AおよびBから出発して円Oの周上を同じ向きにそれぞれ一定の速さで動く2点P,Qがある。Pの速さはQの速さの2倍で、PがAからBまで動くとき、△APQの面積の最大値を求めよ。また,その時の∠BOQの大きさを求めよ。
半径がaである円Oの直径ABの両端AおよびBから出発して円Oの周上を同じ向きにそれぞれ一定の速さで動く2点P,Qがある。Pの速さはQの速さの2倍で、PがAからBまで動くとき、△APQの面積の最大値を求めよ。また,その時の∠BOQの大きさを求めよ。
備考:今回、等速円運動の微分を用いた考え方ではなく、数学ⅠA分野における幾何学的解法を用いた解き方も紹介しています。共通テストでも出題されそうな、円に内接する三角形の面積の最大値に関する問題です。
投稿日:2025.06.10