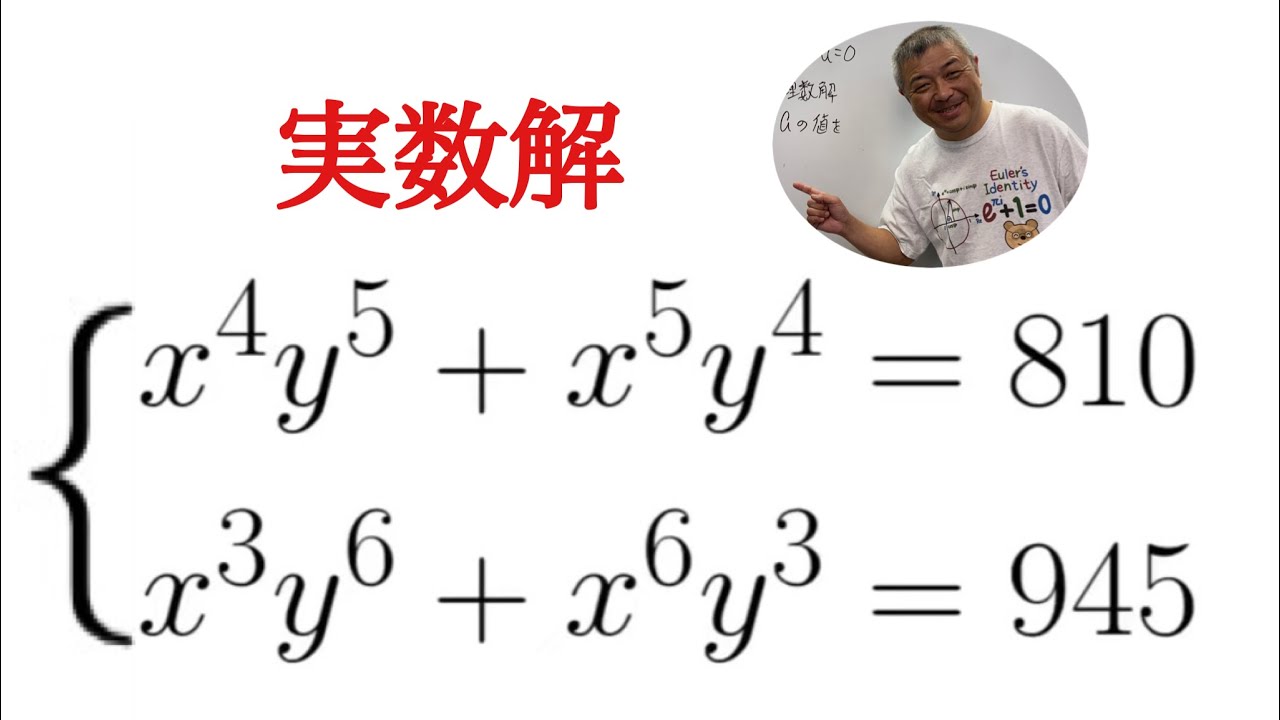【数A】【数と式】つぎの等式のどこが間違えっているでしょう。√(4-2√3)=√(1+3-2√1・3)=√(√1-√3)²=√1-√3=1-√3

問題文全文(内容文)：
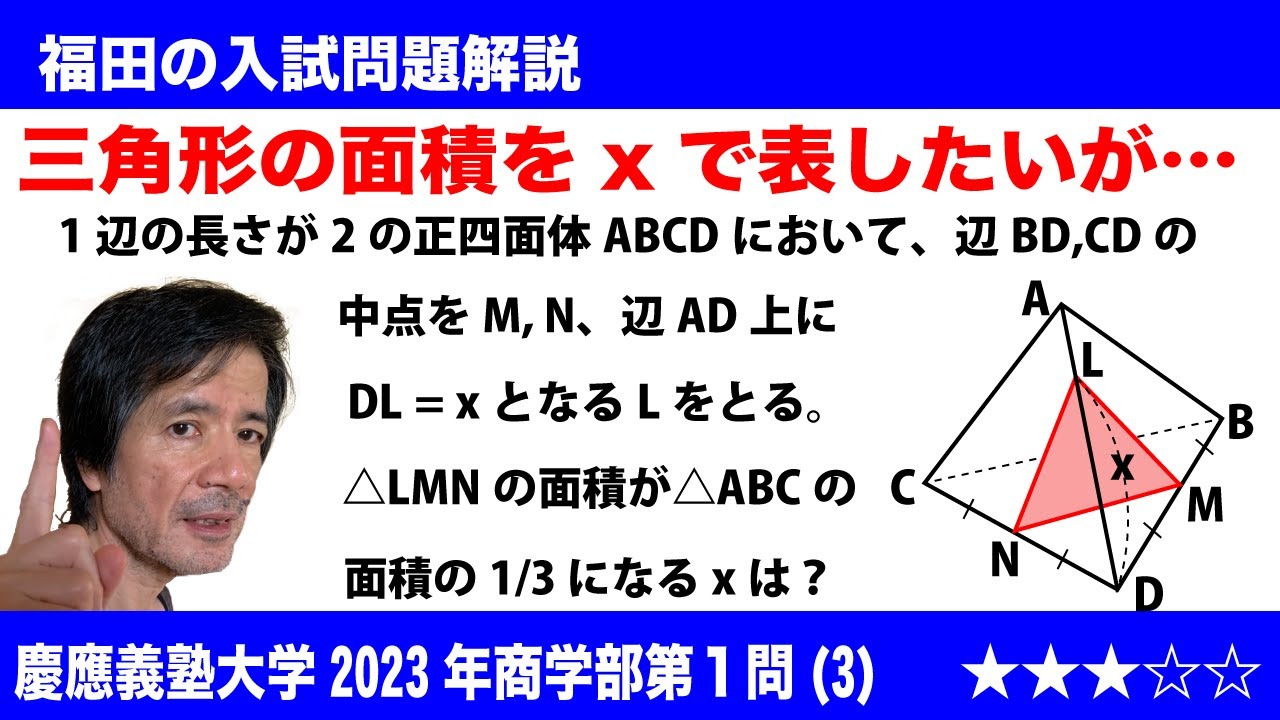
次の二重根号を外しなさい
$\sqrt{4-2\sqrt{3}} $
※解法に間違いがあるので
見つけましょう！

単元： #数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)

教材： #4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#数と式#中高教材

指導講師：理数個別チャンネル

問題文全文(内容文)：
次の二重根号を外しなさい
$\sqrt{4-2\sqrt{3}} $
※解法に間違いがあるので
見つけましょう！

投稿日：2025.07.08

単元： #数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)

指導講師：理数個別チャンネル

問題文全文(内容文)：
実数aに対して2つの集合を$A=｛a-1, 4, a^2-5a+6｝,B=｛1, a^2-4, a^2-7a+12, 4｝$とする。$A∩B=｛0, 4｝$であるとき、aの値を求めよう。

この動画を見る　

単元： #数学(中学生)#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#高校入試過去問(数学)#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$\sqrt{24n}$が整数となるような最小の整数nを求めよ。

大阪教育大学附属高等学校天王寺校舎

この動画を見る　

単元： #数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#2次方程式と2次不等式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：
$\boxed{1}$(1)次の2次方程式において,1つの解が$x=\dfrac{3}{2}-i$であるとき,
実数$a,b$の値を求めよ.ただし,$i$は虚数単位とする.
$-x^2+ax+b=0$

2021中央大経済学部過去問

この動画を見る　

単元： #数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
因数分解せよ
$x^4-7x^2+9$

この動画を見る　

単元： #数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$\frac{1}{2} + \frac{1}{6} + \frac{1}{12} +\frac{1}{20}$

この動画を見る　