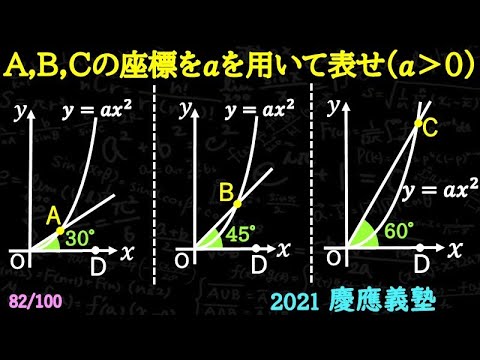
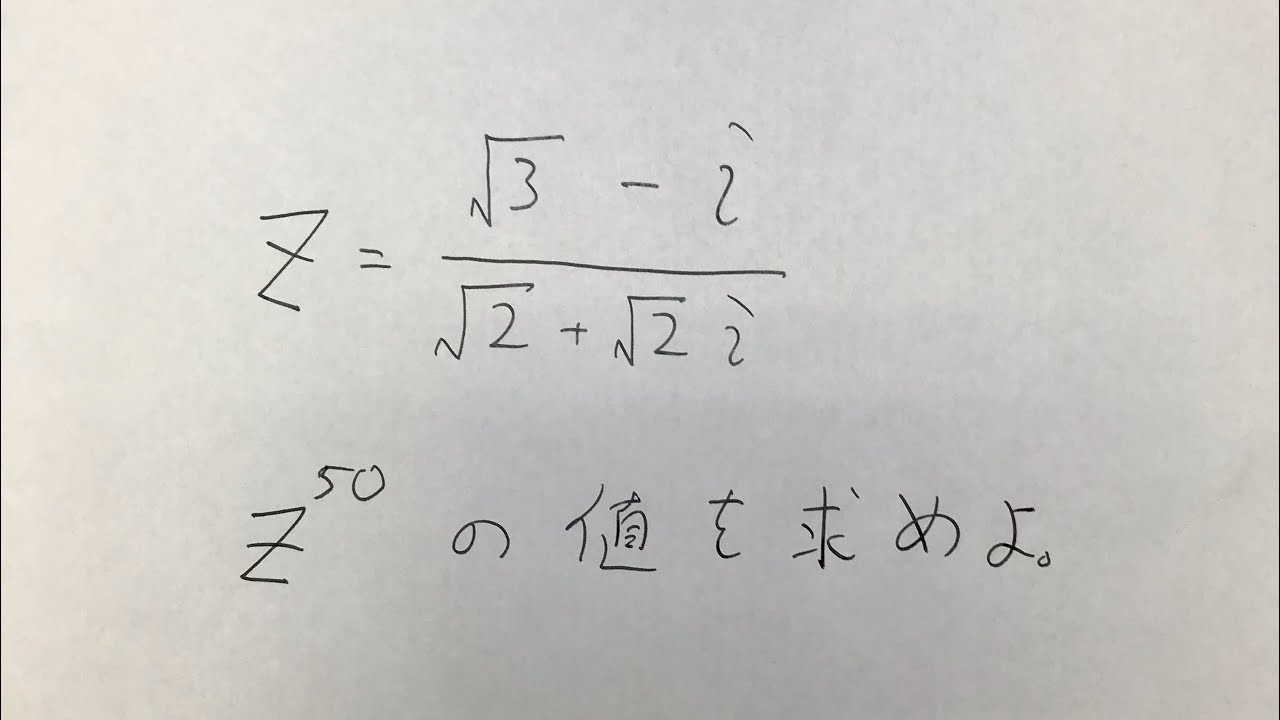問題文全文(内容文):
$f(x)=2\cos \displaystyle \frac{x}{2}+8 \cos \displaystyle \frac{x}{3}$のとりうる範囲は?
出典:2004年国立大学法人信州大学 過去問
$f(x)=2\cos \displaystyle \frac{x}{2}+8 \cos \displaystyle \frac{x}{3}$のとりうる範囲は?
出典:2004年国立大学法人信州大学 過去問
単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#三角関数とグラフ#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=2\cos \displaystyle \frac{x}{2}+8 \cos \displaystyle \frac{x}{3}$のとりうる範囲は?
出典:2004年国立大学法人信州大学 過去問
$f(x)=2\cos \displaystyle \frac{x}{2}+8 \cos \displaystyle \frac{x}{3}$のとりうる範囲は?
出典:2004年国立大学法人信州大学 過去問
投稿日:2019.03.02