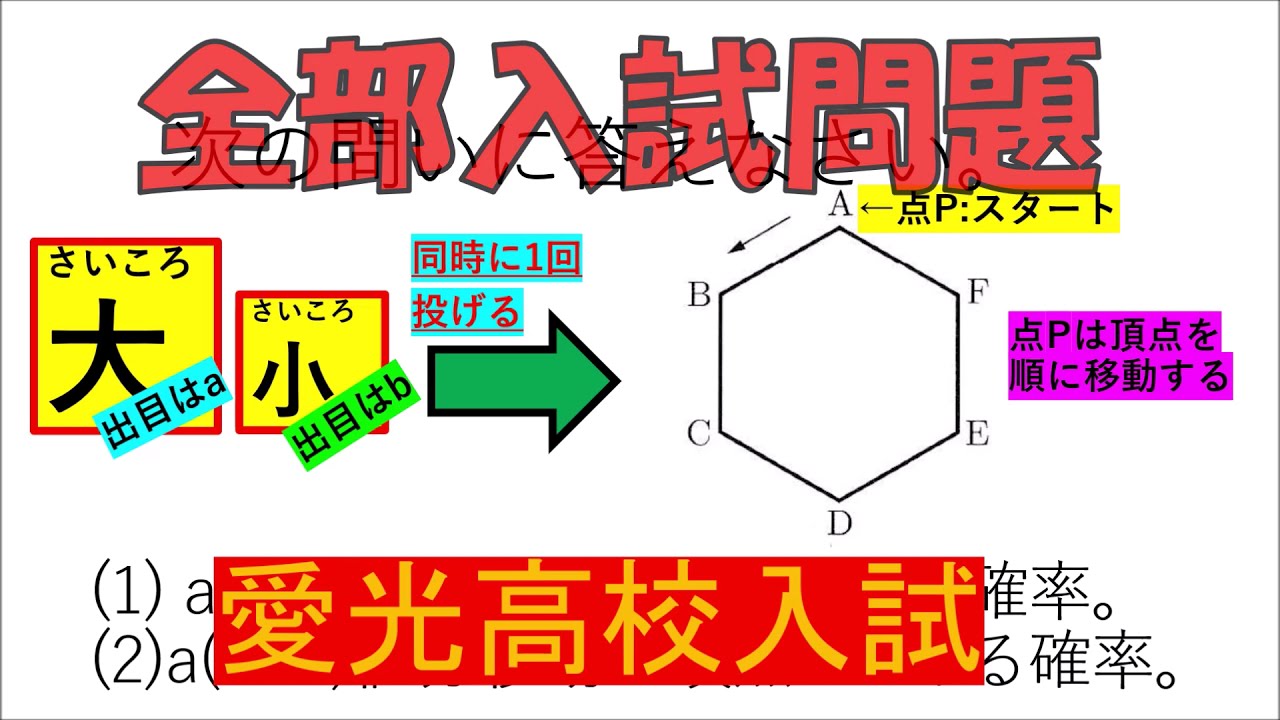
問題文全文(内容文):
右の図Iで、$AD /\!/ BC,AD=AB$で、線分$AC$と線分$BD$の交点を$E$とする。
$\angle BAC=86°、\angle ACB=32°$のとき、
$\angle x,\angle y$の角度を求めなさい。
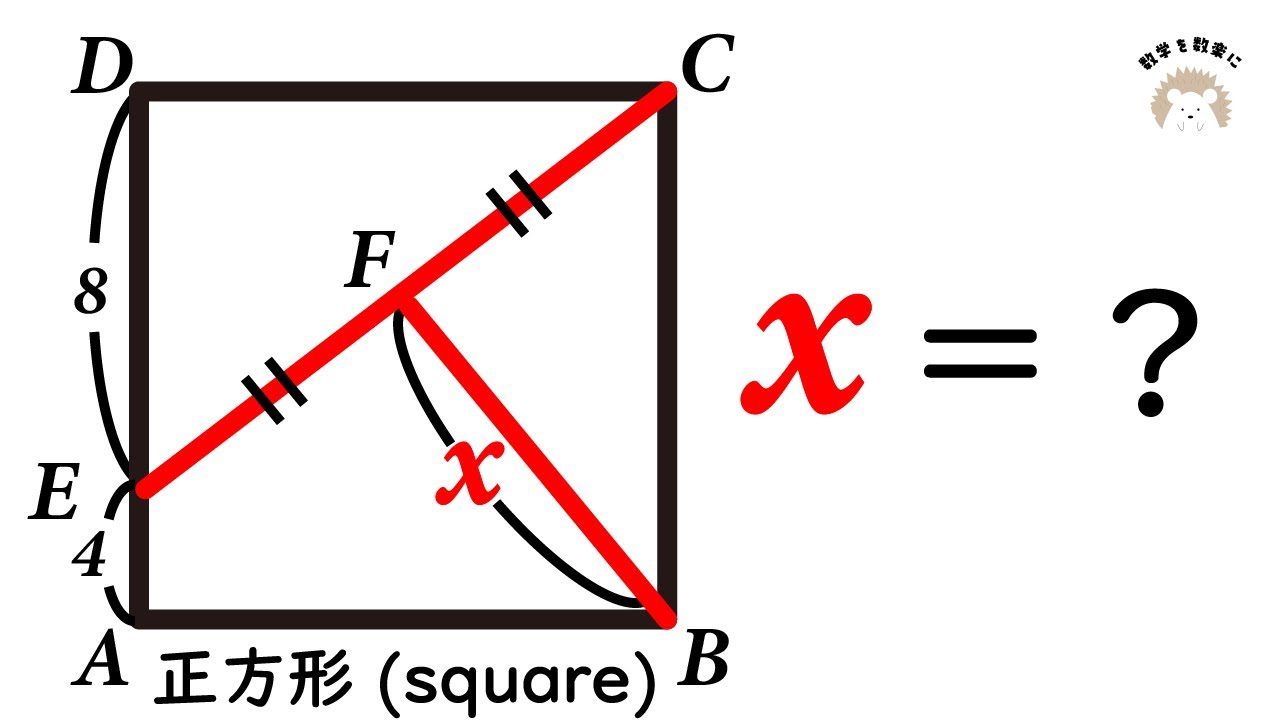
②右の図IIで、$\angle x$を求めなさい。
図は動画内参照
右の図Iで、$AD /\!/ BC,AD=AB$で、線分$AC$と線分$BD$の交点を$E$とする。
$\angle BAC=86°、\angle ACB=32°$のとき、
$\angle x,\angle y$の角度を求めなさい。
②右の図IIで、$\angle x$を求めなさい。
図は動画内参照
単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図Iで、$AD /\!/ BC,AD=AB$で、線分$AC$と線分$BD$の交点を$E$とする。
$\angle BAC=86°、\angle ACB=32°$のとき、
$\angle x,\angle y$の角度を求めなさい。
②右の図IIで、$\angle x$を求めなさい。
図は動画内参照
右の図Iで、$AD /\!/ BC,AD=AB$で、線分$AC$と線分$BD$の交点を$E$とする。
$\angle BAC=86°、\angle ACB=32°$のとき、
$\angle x,\angle y$の角度を求めなさい。
②右の図IIで、$\angle x$を求めなさい。
図は動画内参照
投稿日:2017.07.29