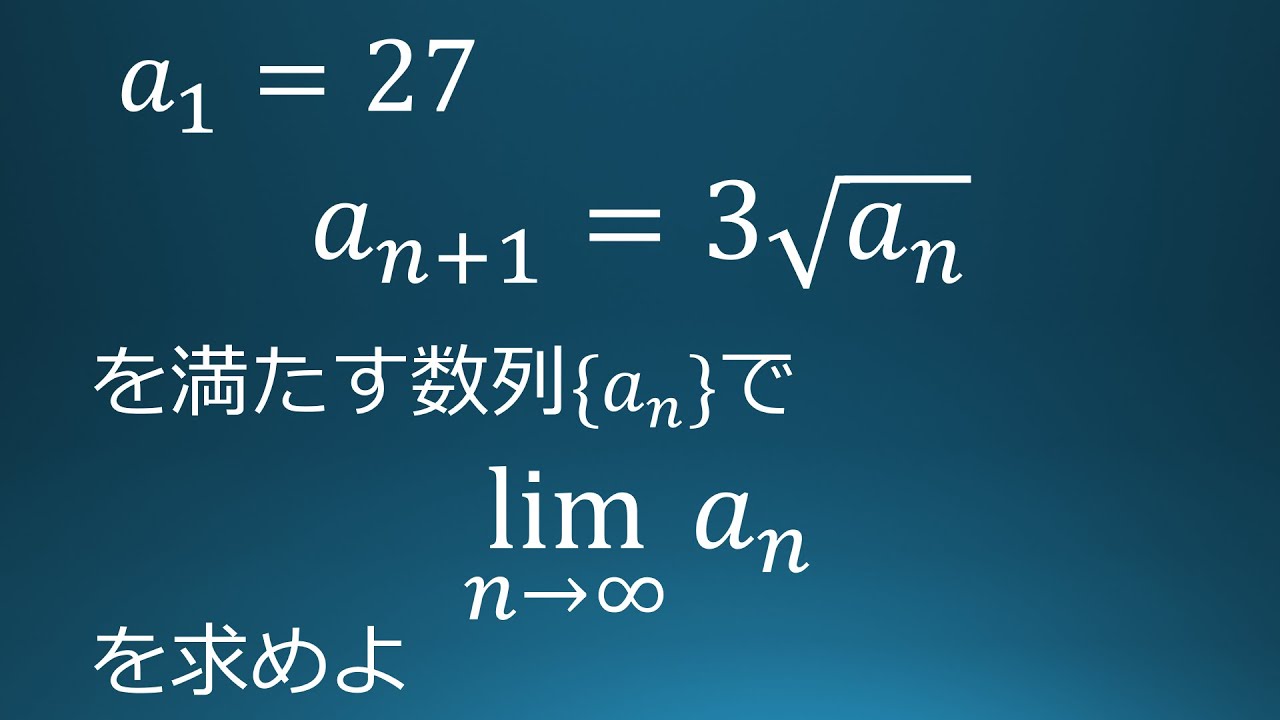【数Ⅲ】極限：関数の極限 x=-tの置換 - 質問解決D.B.（データベース）

問題文全文(内容文)：
次の極限を求めよう。
$\displaystyle \lim_{x\to-\infty}(\sqrt{x^2+2x+3}+x)$

チャプター：

0:00 オープニング
0:05 問題文
0:11 x→-∞のときはx=-tと置換する
0:37 式変形
0:57 有理化
1:30 分母の最高次で割る
2:10 不定形を解消してからx→0に
2:26 名言

単元： #関数と極限#関数の極限#数学(高校生)#数Ⅲ

指導講師：理数個別チャンネル

問題文全文(内容文)：
次の極限を求めよう。
$\displaystyle \lim_{x\to-\infty}(\sqrt{x^2+2x+3}+x)$

投稿日：2021.09.21

単元： #関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
次の関数を微分せよ。

①$y=(x^2-5)^3$

②$y=(x^3+3x)^4$

③$y=(2x^3-3x+1)^5$

④$y=\dfrac{1}{(x^2-3)}^2$

⑤$y=\{(x-1)(x^2+4)\}^4$

この動画を見る　

単元： #関数と極限#数列の極限#数学(高校生)#数Ⅲ

教材： #4S数学#4S数学ⅢのB問題解説#中高教材#極限

指導講師：理数個別チャンネル

問題文全文(内容文)：
次の条件によって定められる数列$\{a_n\}$の極限を求めよ。
$a_1=10, a_{n+1}=2\sqrt{a_n}\quad (n=1,2,3,\cdots)$

この動画を見る　

単元： #関数と極限#関数の極限#数学(高校生)#数Ⅲ

指導講師： 3rd School

問題文全文(内容文)：
極限について解説します。

この動画を見る　

単元： #関数と極限#関数の極限#数学(高校生)#数Ⅲ

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
π=4の証明において誤っている部分を指摘する動画です

この動画を見る　

単元： #関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ

指導講師：理数個別チャンネル

問題文全文(内容文)：
次の関数のグラフをかけ。また，その漸近線を求めよ。
$y=\dfrac{-2x–10}{x+3}$

この動画を見る　