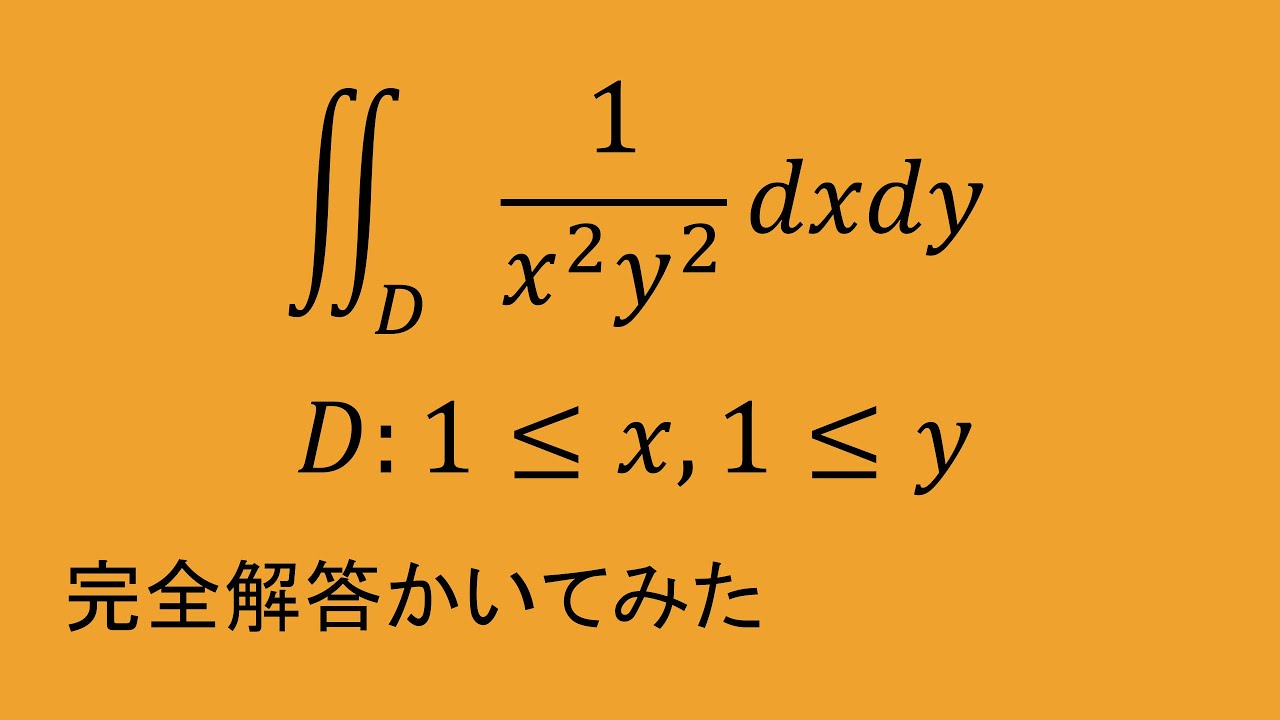問題文全文(内容文):
変数変換(極座標)
$x=rcosθ$ $y=rsinθ$
$∬_D f(x,y)dxdy=∬_D f(rcosθ,rsinθ)rdrdθ$
(1)$∬_D \sqrt{x^2+y^2}dxdy$
$D : 4 \leqq x^2+y^2 \leqq 9$
(2)$∬_D sin\sqrt{x^2+y^2}dxdy$
$D : x^2+y^2 \leqq x^2$
変数変換(極座標)
$x=rcosθ$ $y=rsinθ$
$∬_D f(x,y)dxdy=∬_D f(rcosθ,rsinθ)rdrdθ$
(1)$∬_D \sqrt{x^2+y^2}dxdy$
$D : 4 \leqq x^2+y^2 \leqq 9$
(2)$∬_D sin\sqrt{x^2+y^2}dxdy$
$D : x^2+y^2 \leqq x^2$
単元:
#大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#積分とその応用#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学検定#数学検定1級#数学(高校生)#数Ⅲ#高専(高等専門学校)
指導講師:
ますただ
問題文全文(内容文):
変数変換(極座標)
$x=rcosθ$ $y=rsinθ$
$∬_D f(x,y)dxdy=∬_D f(rcosθ,rsinθ)rdrdθ$
(1)$∬_D \sqrt{x^2+y^2}dxdy$
$D : 4 \leqq x^2+y^2 \leqq 9$
(2)$∬_D sin\sqrt{x^2+y^2}dxdy$
$D : x^2+y^2 \leqq x^2$
変数変換(極座標)
$x=rcosθ$ $y=rsinθ$
$∬_D f(x,y)dxdy=∬_D f(rcosθ,rsinθ)rdrdθ$
(1)$∬_D \sqrt{x^2+y^2}dxdy$
$D : 4 \leqq x^2+y^2 \leqq 9$
(2)$∬_D sin\sqrt{x^2+y^2}dxdy$
$D : x^2+y^2 \leqq x^2$
投稿日:2020.11.04