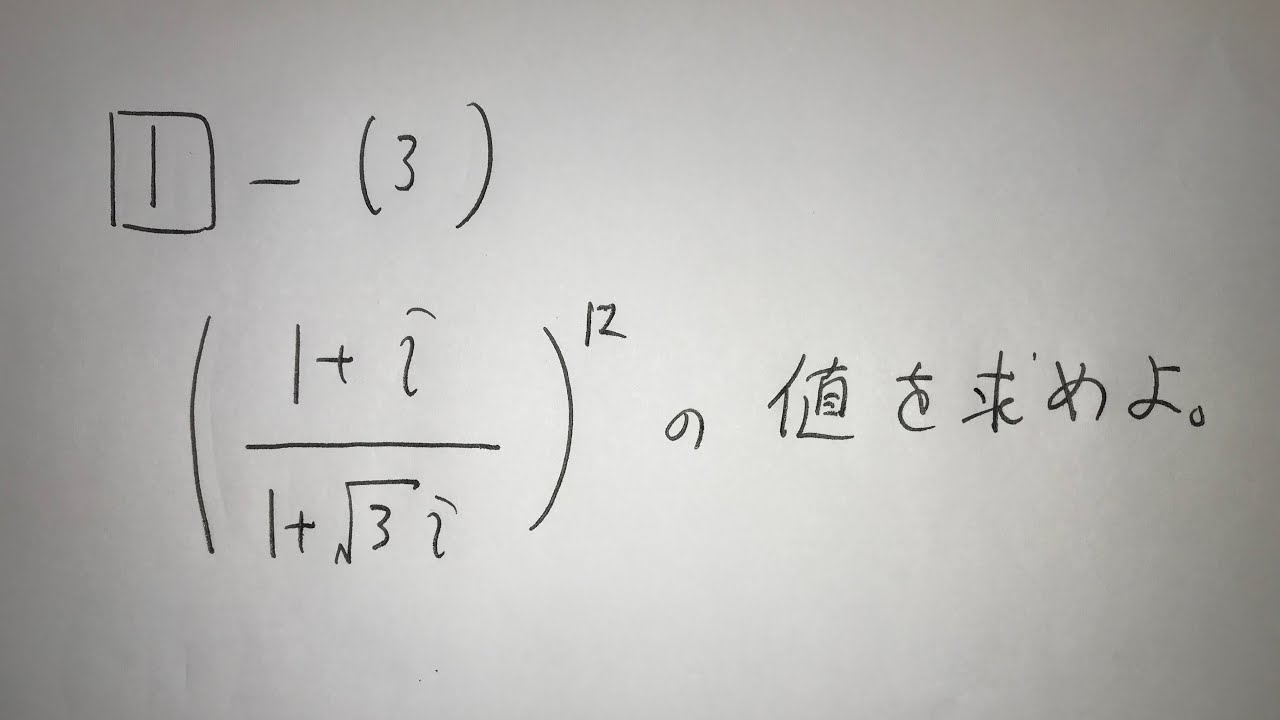問題文全文(内容文):
6⃣$argZ=\frac{4}{3} \pi$ , $arg(1-z)=\frac{\pi}{4}$
$arg \frac{z}{(1-z)^2}$ , |z|を求めよ。
6⃣$argZ=\frac{4}{3} \pi$ , $arg(1-z)=\frac{\pi}{4}$
$arg \frac{z}{(1-z)^2}$ , |z|を求めよ。
単元:
#複素数平面#複素数平面#その他#数学(高校生)#数C#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
6⃣$argZ=\frac{4}{3} \pi$ , $arg(1-z)=\frac{\pi}{4}$
$arg \frac{z}{(1-z)^2}$ , |z|を求めよ。
6⃣$argZ=\frac{4}{3} \pi$ , $arg(1-z)=\frac{\pi}{4}$
$arg \frac{z}{(1-z)^2}$ , |z|を求めよ。
投稿日:2020.08.31