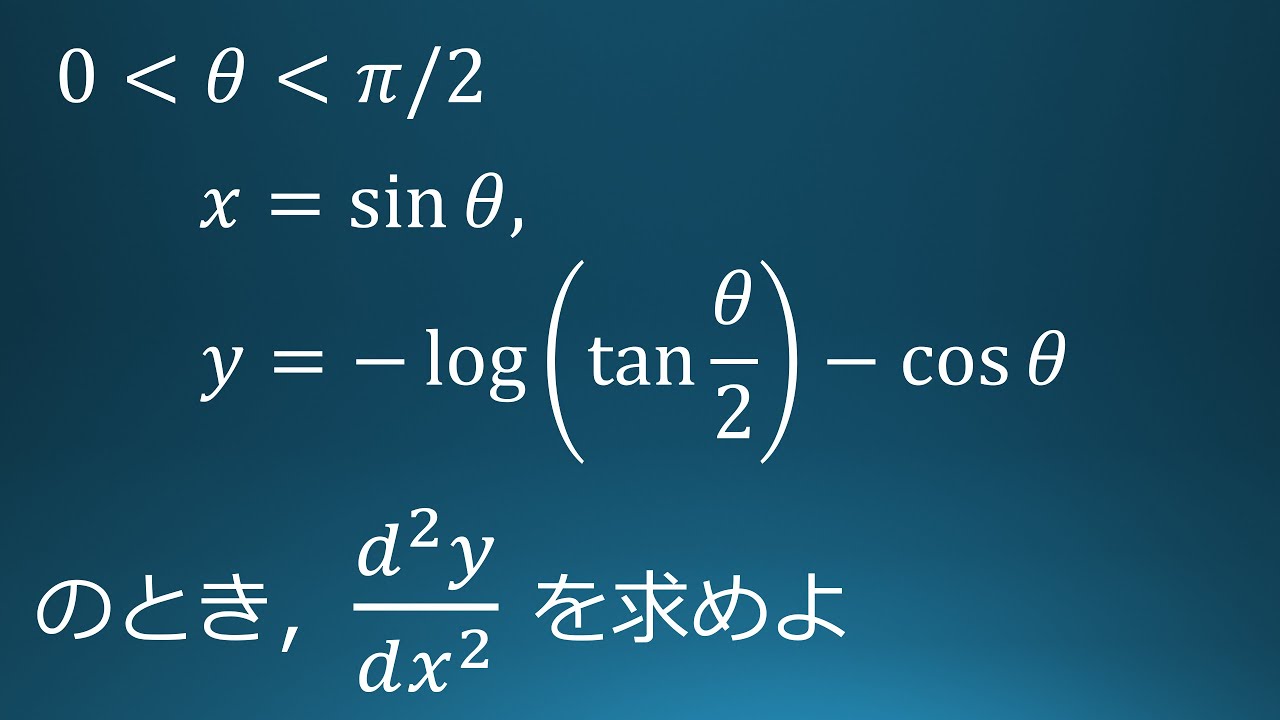名古屋市立（医）lim(x→０)sinx/x=1証明 高校数学 Japanese university entrance exam questions - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数Ⅲ > 微分とその応用 > 微分法 > 名古屋市立（医）lim(x→０)sinx/x=1証明　高校数学 Japanese university entrance exam questions

名古屋市立（医）lim(x→０)sinx/x=1証明　高校数学 Japanese university entrance exam questions

問題文全文(内容文)：
名古屋市立大学過去問題
$\displaystyle \lim_{ x \to 0 } \frac{sinx}{x}=1$
単元： #大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#名古屋市立大学
指導講師： 鈴木貫太郎
問題文全文(内容文)：
名古屋市立大学過去問題
$\displaystyle \lim_{ x \to 0 } \frac{sinx}{x}=1$
投稿日：2018.04.27

＜関連動画＞

【数Ⅲ-174】曲線の長さ①(基本編)

アイキャッチ画像
単元： #微分とその応用#積分とその応用#微分法#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(曲線の長さ①・基本編)

ポイント
曲線$y=f(x) a \leqq x \leqq b$の長さ$L$は $L=$ ①

②$y=x \sqrt{x}(0 \leqq x \leqq \frac{4}{3})$の長さを求めよ。

③$y=\frac{1}{2}x^2-\frac{1}{4}\log x(1 \leqq x \leqq e)$の長さを求めよ。
この動画を見る　

【高校数学】数Ⅲ-116 関数の極値①

アイキャッチ画像
単元： #微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(関数の極値①)
Q.次の関数の極値を求めよ

①$f(x)=\frac{x^2+2x+1}{x^2+1}$

➁$f(x)=x^2e^{-x}$

③$f(x)=\frac{\log x}{x^2}$
この動画を見る　

【数Ⅲ-125】微分の不等式への応用①

アイキャッチ画像
単元： #微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(微分の不等式への応用①)

①$x\gt1$のとき、不等式$2\sqrt{x}\gt\log x$を証明せよ

➁$x\gt1$のとき、不等式$\log x\leqq\frac{x}{e}$を証明せよ
この動画を見る　

福田の1.5倍速演習〜合格する重要問題021〜一橋大学2016年度文系数学第４問〜絶対値の付いた3次関数の最大

アイキャッチ画像
単元： #数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#接線と増減表・最大値・最小値#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数Ⅲ
指導講師： 福田次郎
問題文全文(内容文)：
aを実数とし、$f(x)=x^3-3ax$とする。区間$-1 \leqq x \leqq 1$における
$|f(x)|$の最大値をMとする。Mの最小値とそのときのaの値を求めよ。

2016一橋大学文系過去問
この動画を見る　

福田のおもしろ数学120〜n変数の条件付き最大最小問題

アイキャッチ画像
単元： #微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師： 福田次郎
問題文全文(内容文)：
実数$x_1$,$x_2$,...,$x_n$が$x_1^2$+$x_2^2$+...+$x_n^2$=1　を満たすとき、$x_1^2$+$2x_2^2$+...+$nx_n^2$　の最大値と最小値を求めよ。
この動画を見る　
PAGE TOP