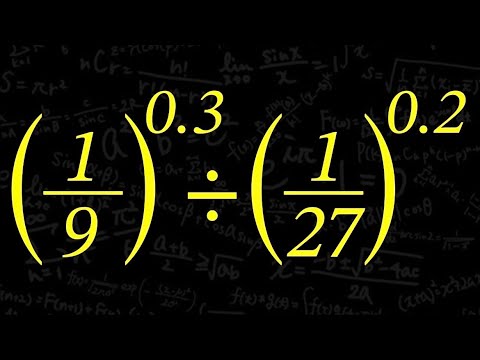【数Ⅰ】数と式：次の計算をせよ。18ab²÷(-3ab)²×(-a²b)³

問題文全文(内容文)：
次の計算をせよ。
$18ab^2\div(-3ab)^2\times(-a^2b)^3$

単元： #数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)

指導講師：理数個別チャンネル

問題文全文(内容文)：
次の計算をせよ。
$18ab^2\div(-3ab)^2\times(-a^2b)^3$

投稿日：2020.09.24

単元： #数Ⅱ#指数関数と対数関数#指数関数#対数関数#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$
\begin{eqnarray}
&&3^a=7^b=441\\
&&\frac{ab}{a+b} = ?

\end{eqnarray}
$

この動画を見る　

単元： #数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$\frac{2^{2022} + 2^{2020}}{10} = 2^▢$
▢=?

この動画を見る　

単元： #数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：
$2^{55},3^{44},4^{33},5^{22}$を小さい順に並べなさい。

この動画を見る　

単元： #数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$2^x=3^y$
$4^{\frac{x}{y}} + 3^{\frac{y}{x}}=?$

この動画を見る　

単元： #数Ⅰ#数Ⅱ#数と式#式の計算（整式・展開・因数分解）#指数関数と対数関数#指数関数#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$\frac{9^5 -6^6}{3^7 - 12^3}$

この動画を見る　