問題文全文(内容文):
高校受験対策・図形39
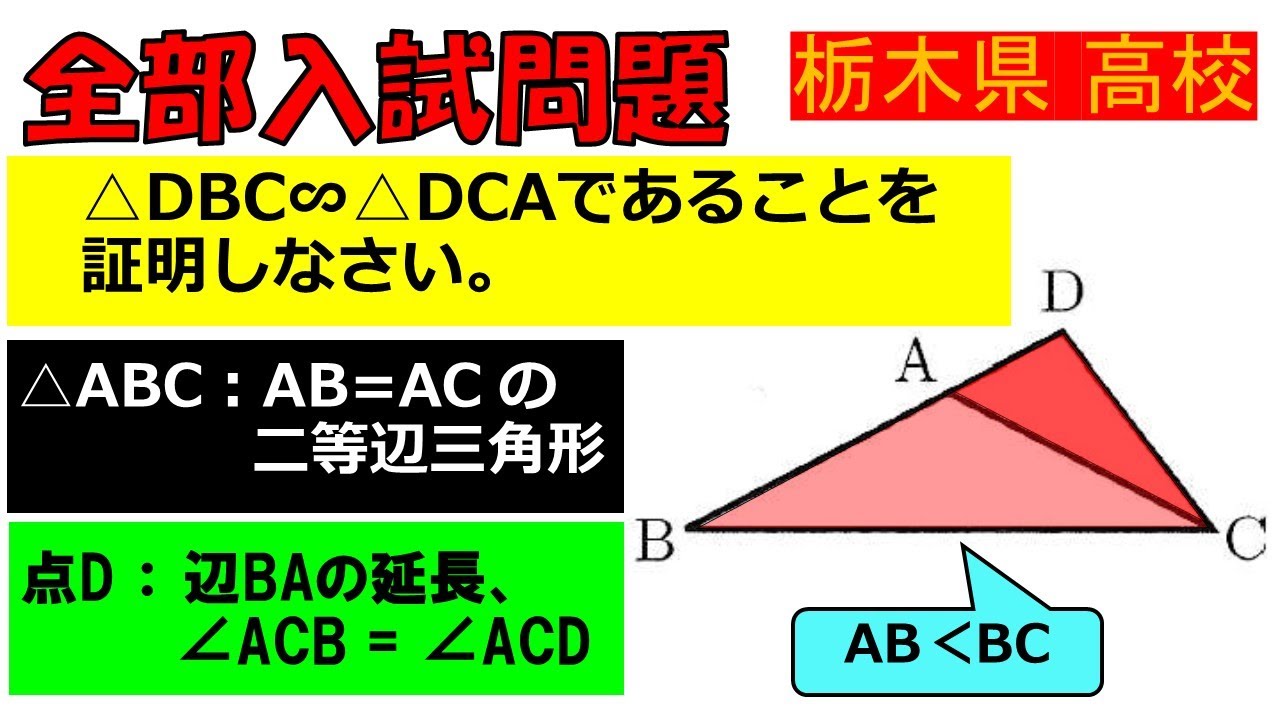
Q.
右の図で、$\triangle ABC$は$\angle BAC=90°$の直角二等辺三角形であり、 $\triangle ADE$は$\angle DAE=90°$の直角二等辺三角形である。
また、点$D$は辺$CB$の延長線上にある。
①$\triangle ADB \equiv \triangle AEC$であることを証明しなさい。
➁$AB=AC=\sqrt{2}cm$、$AD=AE=3cm$のとき、 $DE$の長さを求めなさい。
③➁のとき、$BD$の長さを求めなさい。
高校受験対策・図形39
Q.
右の図で、$\triangle ABC$は$\angle BAC=90°$の直角二等辺三角形であり、 $\triangle ADE$は$\angle DAE=90°$の直角二等辺三角形である。
また、点$D$は辺$CB$の延長線上にある。
①$\triangle ADB \equiv \triangle AEC$であることを証明しなさい。
➁$AB=AC=\sqrt{2}cm$、$AD=AE=3cm$のとき、 $DE$の長さを求めなさい。
③➁のとき、$BD$の長さを求めなさい。
単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形39
Q.
右の図で、$\triangle ABC$は$\angle BAC=90°$の直角二等辺三角形であり、 $\triangle ADE$は$\angle DAE=90°$の直角二等辺三角形である。
また、点$D$は辺$CB$の延長線上にある。
①$\triangle ADB \equiv \triangle AEC$であることを証明しなさい。
➁$AB=AC=\sqrt{2}cm$、$AD=AE=3cm$のとき、 $DE$の長さを求めなさい。
③➁のとき、$BD$の長さを求めなさい。
高校受験対策・図形39
Q.
右の図で、$\triangle ABC$は$\angle BAC=90°$の直角二等辺三角形であり、 $\triangle ADE$は$\angle DAE=90°$の直角二等辺三角形である。
また、点$D$は辺$CB$の延長線上にある。
①$\triangle ADB \equiv \triangle AEC$であることを証明しなさい。
➁$AB=AC=\sqrt{2}cm$、$AD=AE=3cm$のとき、 $DE$の長さを求めなさい。
③➁のとき、$BD$の長さを求めなさい。
投稿日:2021.02.14